ACM专题：字符串匹配算法

字符串匹配问题，无论是编程课还是算法课都会被提及，就连公司笔试、面试也都是热点问题之一。可是奈何当时学习时对于该问题的算法理解并不到位，特此进行总结归纳。
P.s：以下内容主要是对公众号：“程序员小灰”中字符串匹配专题的整理加上自己的理解。原文参考

本文概要：

问题定义
BF算法（暴力求解）
RK算法
BM算法
KMP算法

1. 问题定义

所谓字符串匹配问题，即给定一个字符串A（称：“主串”）和一个字符串B（称：“模式串”），我们需要找出模式串在主串中第一次出现的位置，若模式串未在主串中出现，则返回-1。
举一个例子：

在上图中，字符串B是A的子串，B第一次在A中出现的位置下标是2（字符串的首位下标是0），所以返回 2。
而在下面的例子中：

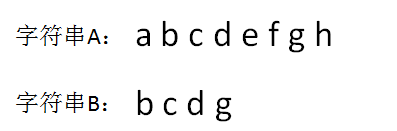
字符串B在A中并不存在，所以返回 -1。

2. BF算法（暴力求解）

Brute Force（暴力算法）的想法其实无须多言，即：遍历主串每一位字符，尝试从头匹配模式串。若与当前主串字符与模式串字符匹配，则尝试用主串中下一位字符去匹配模式串的下一位字符；否则，用主串下一位字符尝试从头匹配模式串。
实例如下：
第一轮，我们从主串的首位开始，把主串和模式串的字符逐个比较。

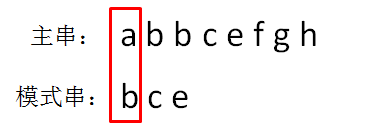
显然，主串的首位字符是a，模式串的首位字符是b，两者并不匹配。

第二轮，我们把模式串后移一位，从主串的第二位开始，把主串和模式串的字符逐个比较

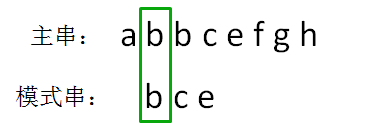
主串的第二位字符是b，模式串的第二位字符也是b，两者匹配，继续比较：

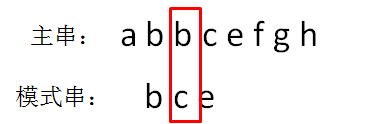
主串的第三位字符是b，模式串的第三位字符也是c，两者并不匹配。
...
重复上述过程，直到找到模式串第一次出现位置，或将主串遍历完毕。

显然，BF算法最大的问题在于对于某些极端情况处理效率极低，如下：

上图的情况，在每一轮进行字符匹配时，模式串的前三个字符a都和主串中的字符相匹配，一直检查到模式串最后一个字符b，才发现不匹配。这样一来，两个字符串在每一轮都需要白白比较4次，显然非常浪费。假设主串的长度是m，模式串的长度是n，那么在这种极端情况下，BF算法的最坏时间复杂度是 $O(mn)$ 。

3. RK算法（Rabin-Karp）

RK算法的核心在于使用哈希散列处理字符串，进而比较两个字符串的哈希值。其实质可看作是对于字符串的一个编码过程。
如果熟悉哈希表的话我们可知，每一个字符串都可以通过某种哈希算法，转换成一个整型数，这个整型数就是hashcode：
$hashcode = hash(string)$

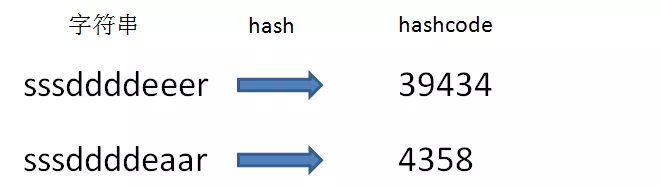
显然，相对于逐个字符比较两个字符串，仅比较两个字符串的hashcode要容易得多。

RK算法流程如下：
给定主串和模式串如下（假定字符串只包含26个小写字母）：

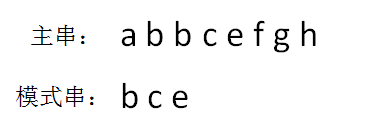
第一步，我们需要生成模式串的hashcode。生成hashcode的算法多种多样，比如：按位相加——这是最简单的方法，我们可以把a当做1，b当做2，c当做3......然后把字符串的所有字符相加，相加结果就是它的hashcode。如：

$bce = 2 + 3 + 5 = 10。$

但是，这个算法虽然简单，却很可能产生hash冲突，比如bce、bec、cbe的hashcode是一样的。
因此，我们不妨考虑将字符串转换成26进制数，既然字符串只包含26个小写字母，那么我们可以把每一个字符串当成一个26进制数来计算。

$bce = 2*(26^2) + 3*26 + 5 = 1435$

这样做的好处是大幅减少了hash冲突，缺点是计算量较大，而且有可能出现超出整型范围的情况，需要对计算结果进行取模。为了方便演示，后续我们采用的是按位相加的hash算法，所以bce的hashcode是10：

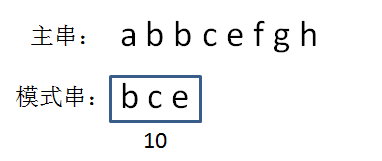
第二步，生成主串当中第一个等长子串的hashcode。由于主串通常要长于模式串，把整个主串转化成hashcode是没有意义的，只有比较主串当中和模式串等长的子串才有意义。因此，我们首先生成主串中第一个和模式串等长的子串hashcode，即abb = 1 + 2 + 2 = 5：

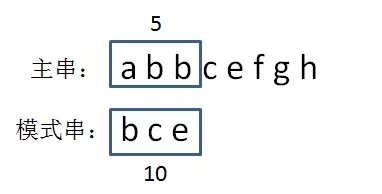
第三步，比较两个hashcode。显然，5！=10，说明模式串和第一个子串不匹配，我们继续下一轮比较。

第四步，生成主串当中第二个等长子串的hashcode。bbc = 2 + 2 + 3 = 7：

...
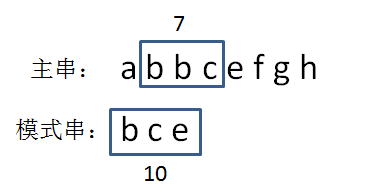
重复以上过程。我们发现，当生成主串当中第三个等长子串的hashcode时，bce= 2 + 3 + 5 = 10：

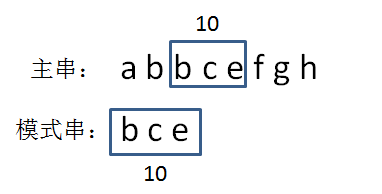
显然，10 ==10，两个hash值相等！这是否说明两个字符串也相等呢？别高兴的太早，由于存在hash冲突的可能，我们还需要进一步验证。
第五步，逐个字符比较两字符串。hashcode的比较只是初步验证，之后我们还需要像BF算法那样，对两个字符串逐个字符比较，最终判断出两个字符串匹配。最后得出结论，模式串bce是主串abbcefgh的子串，第一次出现的下标是2。

通过以上过程，我们不难发现，RK算法本质类似于BF算法，只不过是将字符串的比较转化为先通过哈希值的比较，后进行验证的策略。可能我们会想：每次hash的时间复杂度为 $O(n)$ ，若将全部子串进行hash，最终时间复杂度仍为 $O(mn)$ ，这与BF算法相同。
然而，需要注意的是，每次对主串中的子串进行hash的过程并不独立：我们可以根据前一子串的hashcode进行简单的加减运算即可得到后一子串的hashcode。
综上，由于RK算法计算单个子串hash时间复杂度为 $O(n)$ ，后续子串是增量计算所以整体复杂度仍为 $O(n)$ 。

此外，我们不难想到，由于RK算法核心是使用哈希值，因此该算法的缺点在于哈希冲突。每次哈希冲突（即主串的子串哈希值与模式串相等）时，就需要逐个字符比对，这在极端情况下将退化为BF算法。

MoCuishle