最长回文子串问题，是ACM题库或各大公司笔试/面试中一类经典的问题。该问题在本科阶段的学习中就屡次被提及，但当时并未完全理解。此次对该问题进行一次整理与归纳。

本文概要：

  • 问题定义
  • 求解思路：
    • 暴力求解
    • 动态规划求解
    • 中心扩散法
    • Manacher 算法

1. 问题定义：

定义 1.1 回文串： 是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。（百度百科）
定义 1.2 最长回文子串： 最长回文子串或最长对称因子问题是在一个字符串中查找一个最长的连续的回文的子串，例如“banana”最长回文子串是“anana”。最长回文子串并不一定是唯一的，比如“abracadabra”，没有超过3的回文子串，但是有两个回文字串长度都是3：“ada”和“aca”。

示例 1：
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例 2:
输入: "cbbd"
输出: "bb"

2. 求解思路：

2.1 暴力求解（Brute Force）

直观地，我们可以穷举给定字符串s中全部子串，继而判断当前子串是否符合回文串定义。在所有回文串中找到长度最长的即可。
值得注意的是，在具体实现过程中，我们通过以下技巧来提高算法的效率：

  • 在具体实现时，可以只针对长度大于“当前得到的最长回文子串长度”的子串进行“回文验证”；
  • 在记录最长回文子串的时候，可以只记录“当前子串的起始位置”和“子串长度”，不必做截取。

参考代码如下：

//暴力求解法：
int maxL = 0;
string resStr;
for (int i = 0; i < s.length(); i++)
{
    string str;
    for (int j = i; j < s.length(); j++)
    {
        str += s[j];
        string rstr = str;

        if (maxL < str.length())
        {
            reverse(rstr.begin(), rstr.end());
            if (str == rstr){
                maxL = str.length();
                resStr = str;
            }
        }

    }
}

cout << resStr << endl;

复杂性分析：

  • 时间复杂度：O(N3)O(N^3)，其中N表示给定字符串s的长度。（两重循环+字符串逆序）
  • 空间复杂度：O(1)O(1)。（只记录“当前子串的起始位置”和“子串长度”）

暴力解法时间复杂度高，但是思路清晰、编写简单。因此，可以使用暴力匹配算法检验我们编写的其它算法是否正确。优化的解法在很多时候，是基于“暴力解法”，以空间换时间得到的，因此思考清楚暴力解法，分析其缺点，很多时候能为我们打开思路。

2.2 动态规划（Dynamic programming）

动态规划是算法中一类最基础，同时也是最重要的解题思路之一。判断一个问题是否可以通过动态规划方法求解的核心在于：判读问题是否具有最优子结构性质，即问题的最优解由相关子问题的最优解组合而成，且子问题可单独求解。此处推荐算法领域的经典书籍《算法导论》以及北京航空航天大学童咏昕教授的《算法设计与分析》课程（中国大学MOOC）。
就我本人的理解而言，动态规划方法其本质类似于自动机，即后一状态需参考前一状态（或前多个状态）进行状态转移。在这一过程中，问题核心在于发现状态间转换关系，以及如何实现状态转移。LeetCode中的大神也对动态规划进行了总结（参考文献），见下图：

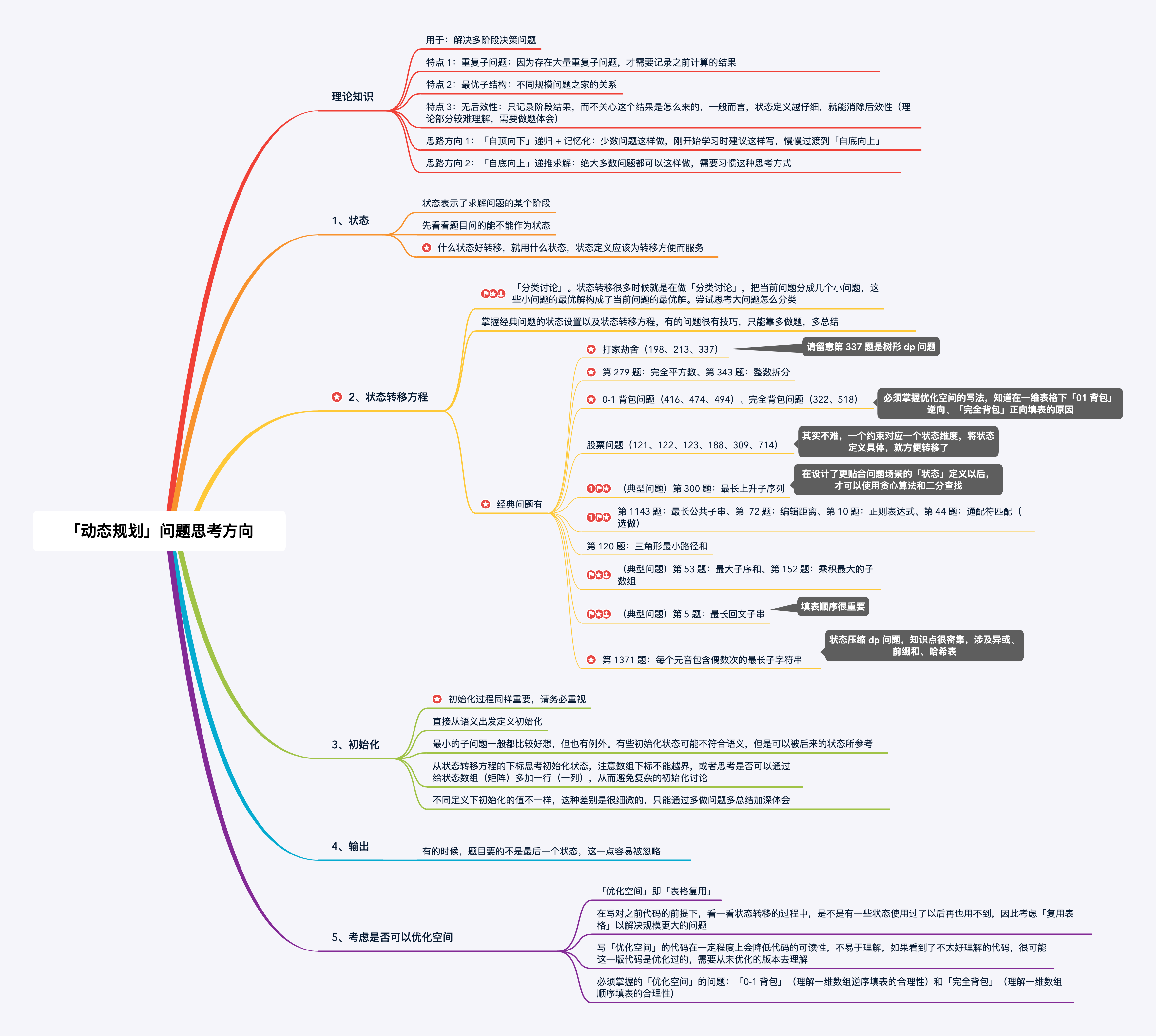
就最长回文子串问题而言，我们不难发现，对于给定字符串s的任意长度大于2的子串s[i][j]（从位置i到位置j构成的子串），其是否为回文子串存在以下关系：

  • s[i][j]s[i][j]是回文串   ⟺  \iff 字符s[i]=s[j]s[i]=s[j]且子串s[i+1][j−1]s[i+1][j-1]是回文串；

因此，我们不难得出该问题的动态规划方法：

  • 1）初始化：初始化一个N*N的矩阵（二维数组）用于表示子串s[i][j]是否为回文串，其中：由于i≤ji\leq j，因此该矩阵为上三角矩阵，且对角线元素均为true。

  • 2）递推公式：

    • 首先，如果子串s[i][j]中的首末字符s[i]≠s[j]s[i]\neq s[j]，则s[i][j]可直接判定为false；
    • 之后，需要判断子串s[i][j]除去首末字符s[i]、s[j]s[i]、s[j]后是否构成区间：
      • 若不构成区间，即：(j−1)−(i+1)+1<2←j−i<3(j-1)-(i+1)+1 < 2\leftarrow j-i < 3：则s[i][j]可判定为true；
      • 若构成区间，即$ j-i \geq 3$：则s[i][j]的结果取决于则s[i+1][j-1]。
      • 注意：每次判定子串s[i][j]是否为回文串后，需再次判断该回文串长度是否大于当前最长回文串长度。若超过当前最长则需要更新。

  • 3）计算顺序：
    该问题的计算顺序是又一难点。不同于一般的动态规划问题：从左至右、从上至下依次根据前一状态计算后一状态，根据该问题的递推公式可知：当前状态（s[i][j]）取决于矩阵中其左下角状态（s[i+1][j-1]）。因此，我们给出该问题两种错误的计算顺序和四种正确的计算顺序：

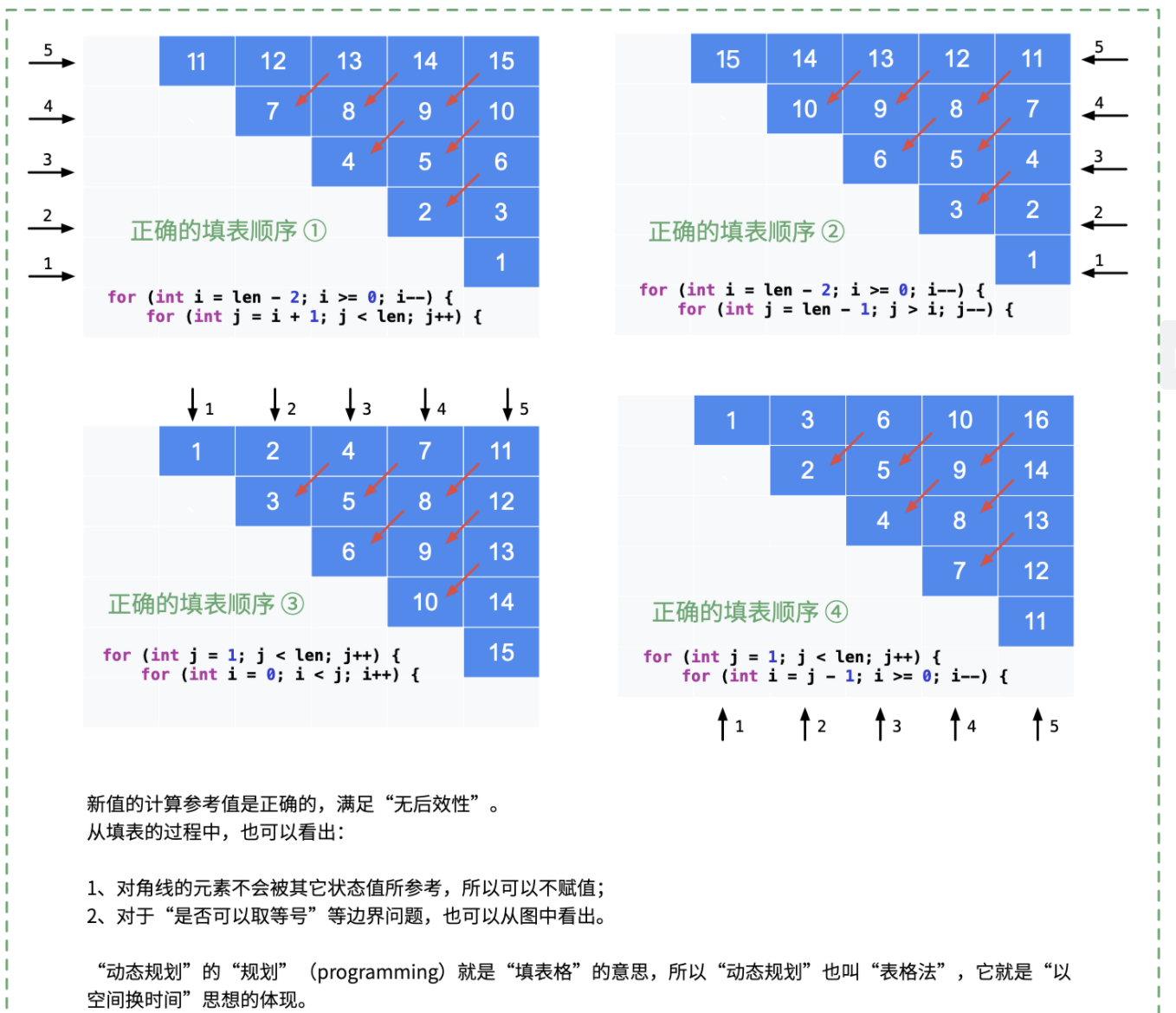
参考代码如下：

int slen = s.length();
int maxLen = 1;
int begin = 0;

if (slen < 2)
{
    cout << s << endl;
}

bool dp[slen][slen];

memset(dp, 0, sizeof(dp));

for (int i = 0; i < slen; i++)
{
    dp[i][i] = true;
}

for (int j = 1; j < slen; j++)
{
    for (int i = 0; i < j; i++)
    {
        if (s[i] != s[j])
        {
            dp[i][j] = false;
        }
        else
        {
            if (j - i < 3) //区间判断：(j-1)-(i+1)+1<2 => j-i<3
            {
                dp[i][j] = true;
            }
            else
            {
                dp[i][j] = dp[i + 1][j - 1];
            }
        }

        if (dp[i][j] && j - i + 1 > maxLen)
        {
            maxLen = j - i + 1;
            begin = i;
        }
    }
}

cout << s.substr(begin, maxLen) << endl;

复杂性分析：

  • 时间复杂度：O(N2)O(N^2);
  • 空间复杂度：O(N2)O(N^2)（二维数组）;

小结（参考）：

  • 我们看到，用「动态规划」方法解决问题，有的时候并不是直接面向问题的。
  • 「动态规划」依然是「空间换时间」思想的体现，并且本身「动态规划」作为一种打表格法，就是在用「空间」换「时间」。
  • 关于「动态规划」方法执行时间慢的说明：
    • 动态规划本质上还是「暴力解法」，因为需要枚举左右边界，有 O(N2)O(N^2)这么多；
    • 以下提供的「中心扩散法」枚举了所有可能的回文子串的中心，有 O(2N)O(2N)这么多，不在一个级别上。

2.3 中心扩散法

中心扩散法其实质是对于朴素的暴力求解法的一种优化：朴素的暴力求解是对于子串左右边界的枚举，而根据回文子串的特性我们不难想到，可对回文“中心位置”进行枚举，并以“中心位置”为中心尝试向左右扩散以得到最长回文子串。

综上，中心扩散法的思路是：遍历每一个可能的中心位置，利用“回文串”中心对称的特点，往两边扩散，看最多能扩散多远。枚举“中心位置”时间复杂度为 O(N)O(N)，从“中心位置”扩散得到“回文子串”的时间复杂度为 O(N)O(N)。因此，中心扩散法时间复杂度为O(N2)O(N^2)。

该方法理解起来并不困难，然而该方法的核心在于如何有效遍历两类回文中心：

  • 奇数回文串的“中心”是一个具体的字符，例如：回文串 "aba" 的中心是字符 "b"；
  • 偶数回文串的“中心”是位于中间的两个字符的“空隙”，例如：回文串串 "abba" 的中心是两个 "b" 中间的那个“空隙”。
    如下图所示：

    因此，可能成为“中心位置”的候选位置如下所示：

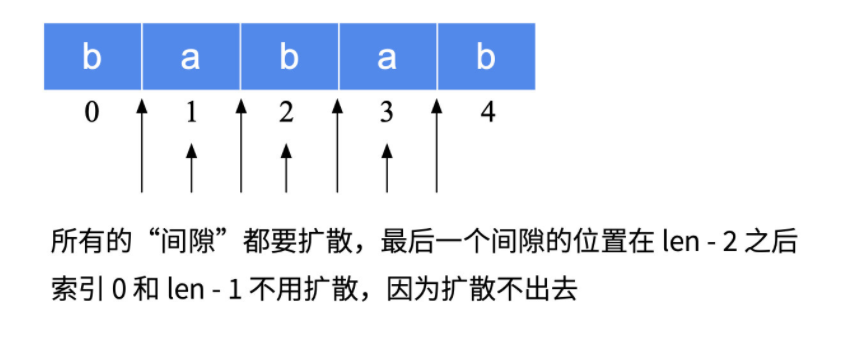
考虑以上情况，参考代码实现如下（原文）：

string centerSpread(string s, int left, int right) {
        // left = right 的时候，此时回文中心是一个空隙，向两边扩散得到的回文子串的长度是奇数
        // right = left + 1 的时候，此时回文中心是一个字符，向两边扩散得到的回文子串的长度是偶数
        int size = s.size();
        int i = left;
        int j = right;
        while (i >= 0 && j < size) {
            if (s[i] == s[j]) {
                i--;
                j++;
            } else {
                break;
            }
        }
        // 这里要小心，跳出 while 循环时，恰好满足 s.charAt(i) != s.charAt(j)，因此不能取 i，不能取 j
        return s.substr(i + 1, j - i - 1);
    }

string longestPalindrome(string s) {
        // 特判
        int size = s.size();
        if (size < 2) {
            return s;
        }

        int maxLen = 1;
        string res = s.substr(0, 1);

        // 中心位置枚举到 len - 2 即可
        for (int i = 0; i < size - 1; i++) {
            string oddStr = centerSpread(s, i, i);
            string evenStr = centerSpread(s, i, i + 1);
            string maxLenStr = oddStr.size() > evenStr.size() ? oddStr : evenStr;
            if (maxLenStr.length() > maxLen) {
                maxLen = maxLenStr.size();
                res = maxLenStr;
            }
        }
        return res;
    }

2.4 Manacher 算法

Manacher 算法其时间复杂度为O(N)O(N)，然而其本身较为复杂。以下仅是自己的理解综合参考文献进行的归纳。

Manacher 算法其核心类似于著名的字符串匹配问题中的KMP算法：基于中心扩展算法，在下一次扩展时充分利用上一次扩展中的可用信息。
在介绍Manacher 算法具体流程之前，需要引入臂长的概念。所谓臂长，即表示中心扩展算法向外扩展的长度。如果一个位置的最大回文字符串长度为 2 * L + 1 ，其臂长为 L。以Leetcode中的示例为例：给定字符串s="ebabababe"，对于位置j=4（s[j]=s[4]='a'）而言，其臂长L=4:

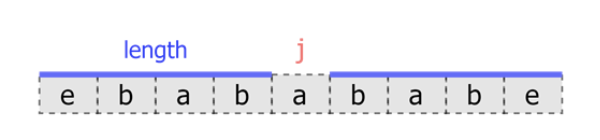
Manacher 算法其出发点在于，从位置为i的位置进行中心扩展，能否借助之前得到的位置为j的中心扩展中的信息。答案是肯定的。具体来说，如果位置 j 的臂长为L，并且有 j + L > i，如下图所示：

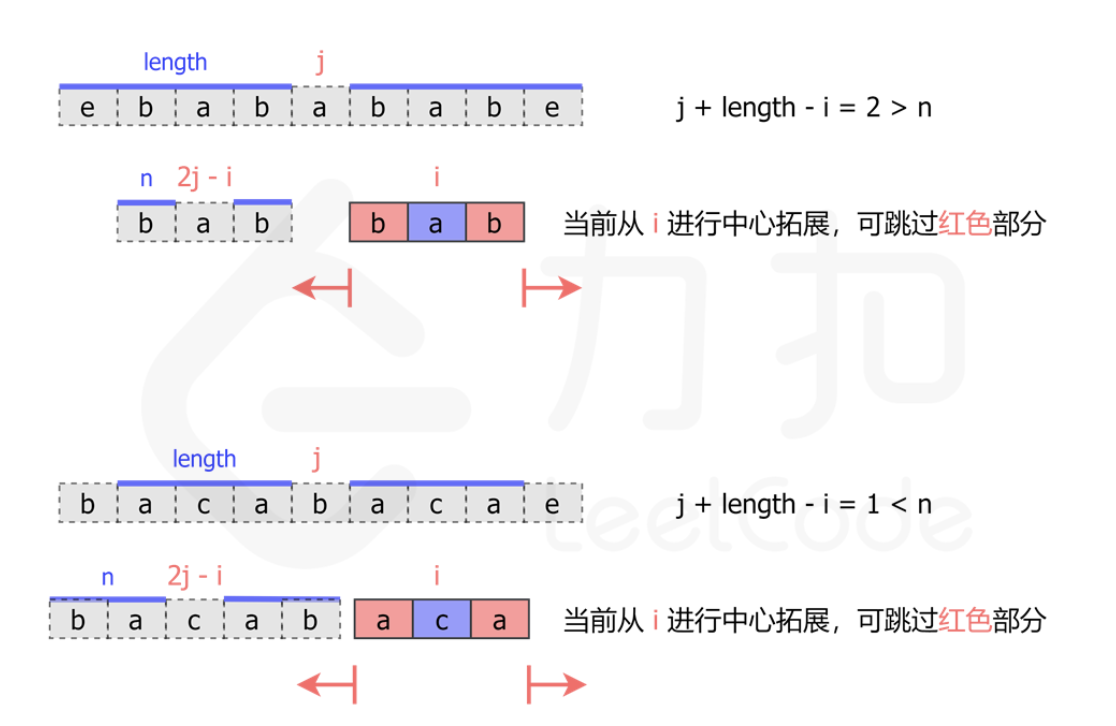
当在位置 i 开始进行中心拓展时，我们可以先找到 i 关于 j 的对称点i′=2∗j−ii'=2 * j - i。那么如果点 i′i'的臂长等于 n，我们就可以知道，点 i 的臂长至少为 min(j+L−i,n)min(j + L - i, n)。那么我们就可以直接跳过 i 到 i + min(j + L - i, n) 这部分，从 i + min(j + L - i, n) + 1 开始拓展。

以上图为例，j=4,L=4：
若i=6，可知i′=2i'=2，且i′i'的臂长n=1。由于min(j+L−i,n)=min(2,1)=1min(j + L - i, n)=min(2,1)=1，所以我们就可以直接跳过 i=6 到 i + min(j + L - i, n) =7 这部分，从位置 i + min(j + L - i, n) + 1 =8 开始拓展。

显然，以上的处理仅针对字符串长度为奇数。而对于字符串长度为偶数的情况，我们可以通过一个简单的小技巧即可完成两种情况的统一：我们向字符串的头尾以及每两个字符中间添加一个特殊字符 #，比如字符串 aaba 处理后会变成 #a#a#b#a#。那么原先长度为偶数的回文字符串 aa 会变成长度为奇数的回文字符串 #a#a#，而长度为奇数的回文字符串 aba 会变成长度仍然为奇数的回文字符串 #a#b#a#，我们就不需要再考虑长度为偶数的回文字符串了。

参考代码如下：

int expand(const string& s, int left, int right) {
        while (left >= 0 && right < s.size() && s[left] == s[right]) {
            --left;
            ++right;
        }
        return (right - left - 2) / 2;
    }

    string longestPalindrome(string s) {
        int start = 0, end = -1;
        string t = "#";
        for (char c: s) {
            t += c;
            t += '#';
        }
        t += '#';
        s = t;

        vector<int> arm_len;
        int right = -1, j = -1;
        for (int i = 0; i < s.size(); ++i) {
            int cur_arm_len;
            if (right >= i) {
                int i_sym = j * 2 - i;
                int min_arm_len = min(arm_len[i_sym], right - i);
                cur_arm_len = expand(s, i - min_arm_len, i + min_arm_len);
            }
            else {
                cur_arm_len = expand(s, i, i);
            }
            arm_len.push_back(cur_arm_len);
            if (i + cur_arm_len > right) {
                j = i;
                right = i + cur_arm_len;
            }
            if (cur_arm_len * 2 + 1 > end - start) {
                start = i - cur_arm_len;
                end = i + cur_arm_len;
            }
        }

        string ans;
        for (int i = start; i <= end; ++i) {
            if (s[i] != '#') {
                ans += s[i];
            }
        }
        return ans;
    }