MoCuishle

整理一下关于哈希冲突的解决策略

1. 开放地址法（再散列法）

当关键字key的哈希地址p=H（key）出现冲突时，以p为基础，产生另一个哈希地址p1，如果p1仍然冲突，再以p为基础，产生另一个哈希地址p2，…，直到找出一个不冲突的哈希地址pi ，将相应元素存入其中。这种方法有一个通用的再散列函数形式：

$Hi=(H(key)+d_i)$

其中$H(key)$为哈希函数，m 为表长，$d_i$称为增量序列。增量序列的取值方式不同，相应的再散列方式也不同。主要有以下几种：

1.1 线性探测法：

$d_i=1,2,3,\dotsb,m−1$

这种方法的特点是：冲突发生时，顺序查看表中下一单元，直到找出一个空单元或查遍全表。
建立在两个假设基础上：（1）表格足够大（2）每个元素都能够独立

1.2 二次探测法：

$d_i=1^2，−1^2，2^2，−2^2，…，k^2，−k^2 \ (k\leq m/2)$

这种方法的特点是：冲突发生时，在表的左右进行跳跃式探测，比较灵活。

1.3 伪随机探测法：

$d_i=伪随机数序列$

具体实现时，应建立一个伪随机数发生器，（如i=(i+p)%m），并给定一个随机数做起点。

1.4 示例：

已知哈希表长度m=11，哈希函数为：H（key）= key % 11，则对于序列$\{47,26,60,69\}$有
H（47）=3，H（26）=4，H（60）=5，H（69）=3，69与47冲突:

• 线性探测再散列处理冲突：
  下一个哈希地址为H1=（3+1）%11=4,
  仍然冲突，再找下一个哈希地址为H2=（3+2）%11=5
  还是冲突，继续找下一个哈希地址为H3=（3+3）%11=6
  此时不再冲突，将69填入6号单元。
  平均查找长度为 (1+1+1+4)/4=7/4

• 用二次探测再散列处理冲突：
  下一个哈希地址为$H1=（3+1^2）$
  仍然冲突，再找下一个哈希地址为$H2=（3−1^2）$
  此时不再冲突，将69填入2号单元
  平均查找长度为 (1+1+1+3)/4=6/4

• 用伪随机探测再散列处理冲突：
  若伪随机数序列为：2，5，9，……..，
  则下一个哈希地址为H1=（3+2）%11=5
  仍然冲突，再找下一个哈希地址为H2=（3+5）%11=8
  此时不再冲突，将69填入8号单元。
  平均查找长度为 (1+1+1+3)/4=6/4

2. 链地址法（拉链法）：

这种方法的基本思想是将所有哈希地址为i的元素构成一个称为同义词链的单链表，并将单链表的头指针存在哈希表的第i个单元中，因而查找、插入和删除主要在同义词链中进行。

例如，已知一组关键字（32，40，36，53，16，46，71，27，42，24，49，64），哈希表长度为13，哈希函数为：H（key）=key%13，如图：

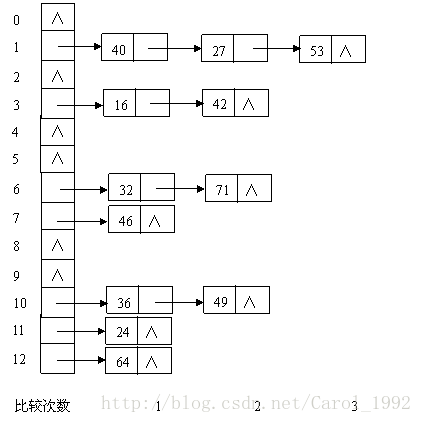
由于链表的特点是：寻址困难，插入和删除容易，链地址法适用于经常进行插入和删除的情况。

3. 公共溢出区法：

将哈希表分为基本表和溢出表两部分，凡是和基本表发生冲突的元素，一律填入溢出表。

4. 再哈希法：

这种方法是同时构造多个不同的哈希函数：

$H_i=RH_i(key),\ i=1,2,\dotsb , k$

当哈希地址$H_i=RH_1(key)$发生冲突时，再计算$H_i=RH_2(key)$……，直到冲突不再产生。
这种方法不易产生聚集，但增加了计算时间。

P.s hash法查找效率：

我们可以看到，哈希表存储和查找数据的时候分为两步，第一步为将关键字通过哈希函数映射为数组中的索引， 这个过程可以认为是只需要常数时间的。第二步是，如果出现哈希值冲突，如何解决，对于常用的拉链法和线性探测法我们可以讨论得到：

对于拉链法，查找的效率在于链表的长度，一般的我们应该保证长度在m /8~m /2之间，如果链表的长度大于m /2，我们可以缩小链表长度。如果长度在0~M/8时，我们可以扩充链表。

对于线性探测法，需要调整数组长度，但是动态调整数组的大小需要对所有的值从新进行重新散列并插入新的表中。因此，拉链法的查找效率要比线性探测法高。

不管是拉链法还是散列法，这种动态调整链表或者数组的大小以提高查询效率的同时，还应该考虑动态改变链表或者数组大小的成本。散列表长度加倍的插入需要进行大量的探测， 这种均摊成本不能忽略。

此外，hash表的查找效率还和负载因子有关，**负载因子即hash表的记录数与哈希表的长度的比值，一般为0.7左右。**冲突性的概率与负载因子的大小成正比，因此负载因子越大，查找效率越低。