本文从“柯尼斯堡七桥问题”作为引入,介绍“图”这一重要数据类型上的相关的一些定义、定理。
<本文涉及的概念均采用目前公认的定义、及描述方法>
本文涉及知识点:
- 图的概念:
- 图的定义、相邻与关联;
- 顶点的度与图的度、握手定理;
- 路径与环路;
- 连通、连通分量;
- 子图、生成子图、树
- 图的表示:
- 邻接链表
- 邻接矩阵
1. 引入——柯尼斯堡七桥问题
1.1. 问题描述:七座桥连接河岸和两个小岛,步行者怎样才能不重复、不遗漏地一次走完七座桥?
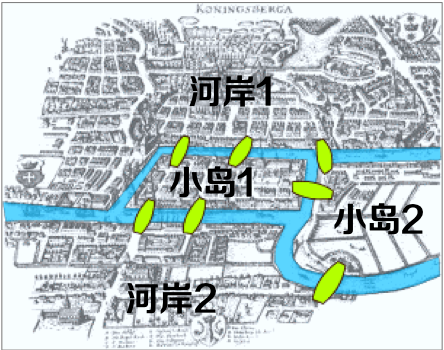
柯尼斯堡七桥问题被认为是图论问题的起源,该问题经过抽象后,可得到仅保留节点和边的结构,该结构被称之为“图”。
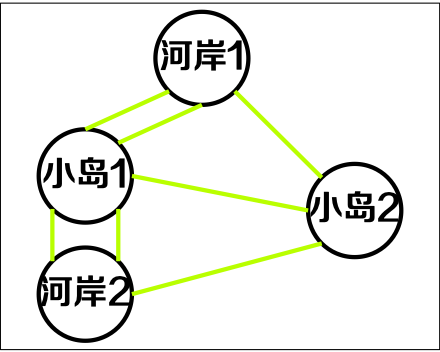
1.2. 图的应用:
- 计算机网络:因特网,万维网...
- 交通出行:地铁交通网,道路交通网...
- 社交网络:微博、微信...
2. 概念——图的定义
2.1. 图:
图可以表示为一个二元组,其中:
* 表示非空顶点集,其元素称为顶点(Vertex);
* 表示边集,其元素称为(Edge)。其中,表示一条边,其中𝒖∈𝑽, 𝒗∈𝑽, 𝒆∈𝑬。
2.2. 无向图 & 有向图:
-
无向图(Undirected Graph):
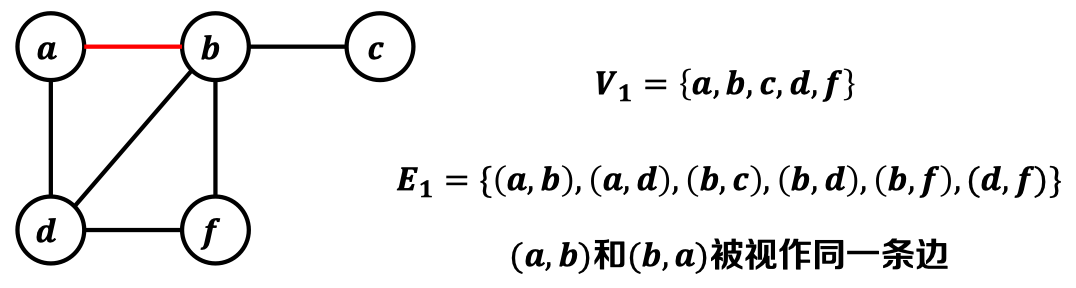
-
有向图(Directed Graph):

2.3. 相邻 & 关联:
-
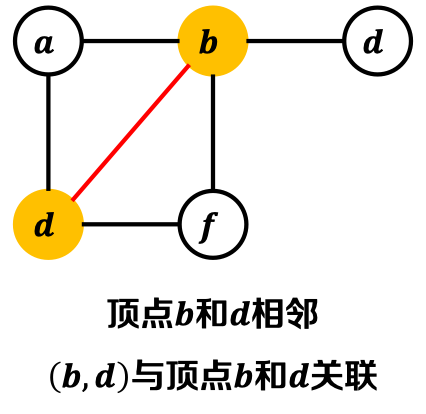
相邻(Adjacent):边(𝒖, 𝒗)连接的顶点𝒖和𝒗相邻;
-
关联(Incident):边(𝒖, 𝒗)和其连接的顶点𝒖(或𝒗)相互关联
2.4. 度: -
顶点的度(Degree of a Vertex):
- 顶点𝒗的度:𝒅𝒆𝒈(𝒗)是𝒗关联的边数;
-
图的度(Degree of a Graph):
- 图𝑮 =< 𝑽, 𝑬 >的度,是图各顶点的度之和——𝒅𝒆𝒈(𝑮) =𝒅𝒆𝒈(𝒗)
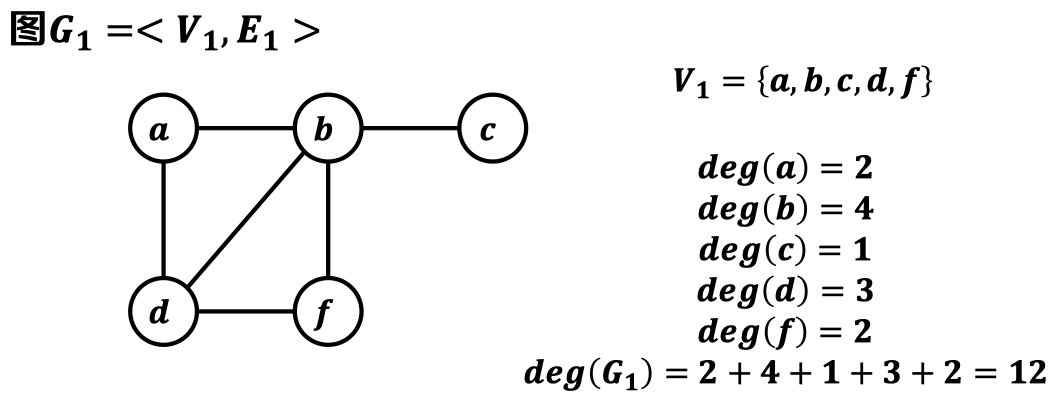
- 图𝑮 =< 𝑽, 𝑬 >的度,是图各顶点的度之和——𝒅𝒆𝒈(𝑮) =𝒅𝒆𝒈(𝒗)
-
握手定理(Handshaking Lemma):无向图的度是边数的两倍,𝒅𝒆𝒈(𝑮) = 𝟐|𝑬|
- 利用握手定理解柯尼斯堡七桥问题:根据问题可知,从起点出发,经过图中所有边,最终到达终点:
- 起点:第一步需要从一条边离开;
- 终点:最后一步需要从一条边到达;
- 其他顶点:从一条边到达后,需要从另一条边离开。因此,其他顶点的度为必须为偶数,否则无法离开。
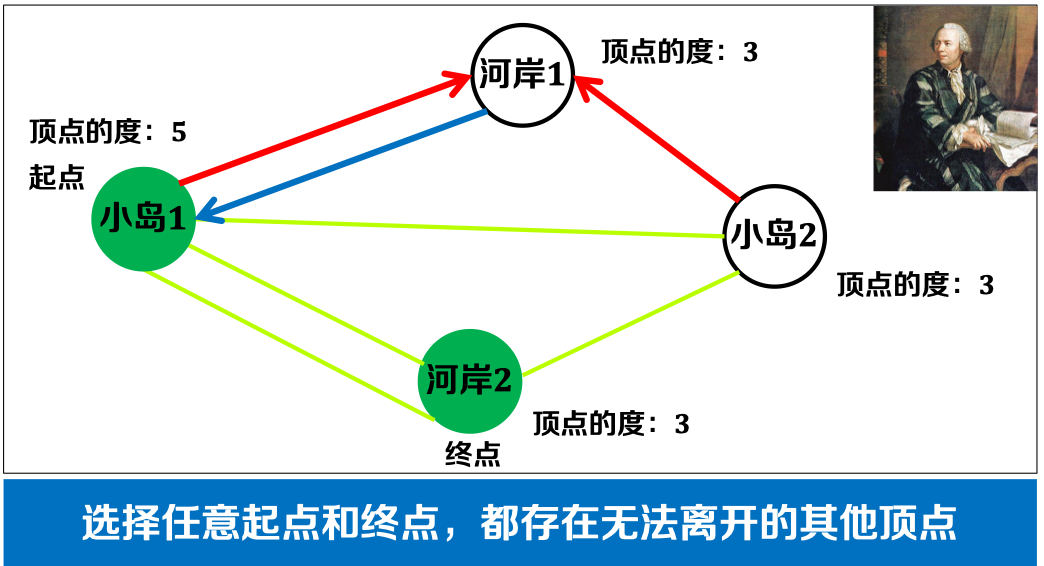
综上,柯尼斯堡七桥问题无解
2.5. 路径(Path):
- 图中一个的顶点序列,称为从到的路径;
- 路径包含顶点,和边;
- 存在路径,则节点与可达(reachability);
- 如果互不相同,则该路径是简单的。
2.6. 环路(Cycle)& 无环图(Acyclic Graph): - 如果路径中,且至少包含一条边,则该路径构成环路;
- 如果互不相同,则该环路是简单的;
- 无环图——图中不存在环路。
2.7. 连通(Connectivity)& 连通分量(Connected Components): - 如果图的任意对顶点互相可达,则称该图是连通的,反之称为非连通
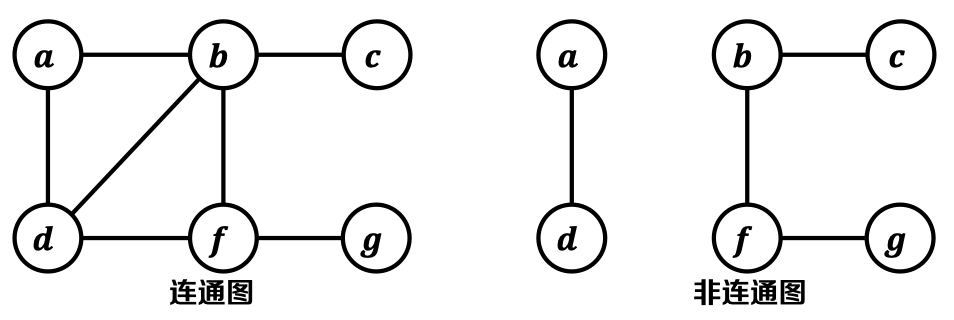
- 根据是否连通将顶点进行分组,相互可达的顶点集称为连通分量
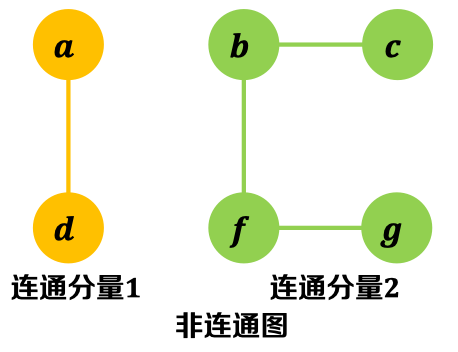
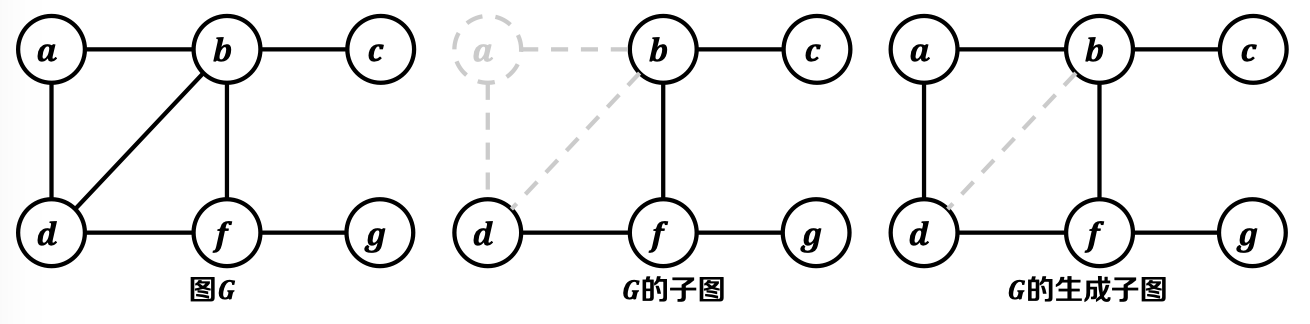
2.8. 子图(Subgraph)& 生成子图(Spanning Subgraph): - 子图:如果𝑽 ′ ⊆ 𝑽, 𝑬′ ⊆ 𝐄,则称图是图的一个子图;
- 生成子图:如果𝑽 ′ = 𝑽, 𝑬′ ⊆ 𝐄,则称图是图的一个生成子图;
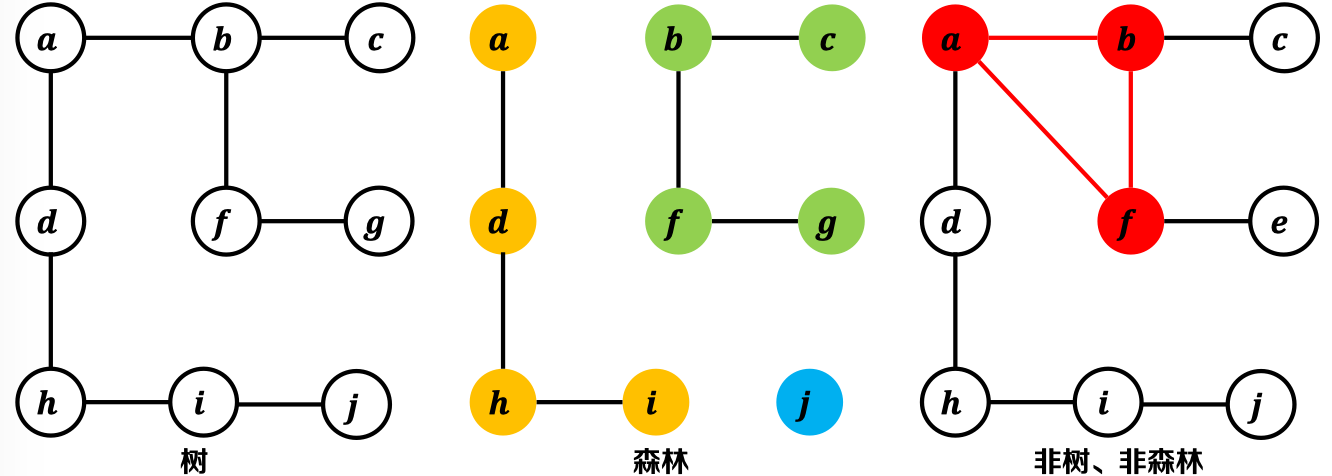
2.9. 树(Tree)& 森林(Forest): - 树——可以看作是一种特殊的连通、无环图——,其中
- 森林——一至多棵树组成的无环图。
3. 表示——常用的表示方式
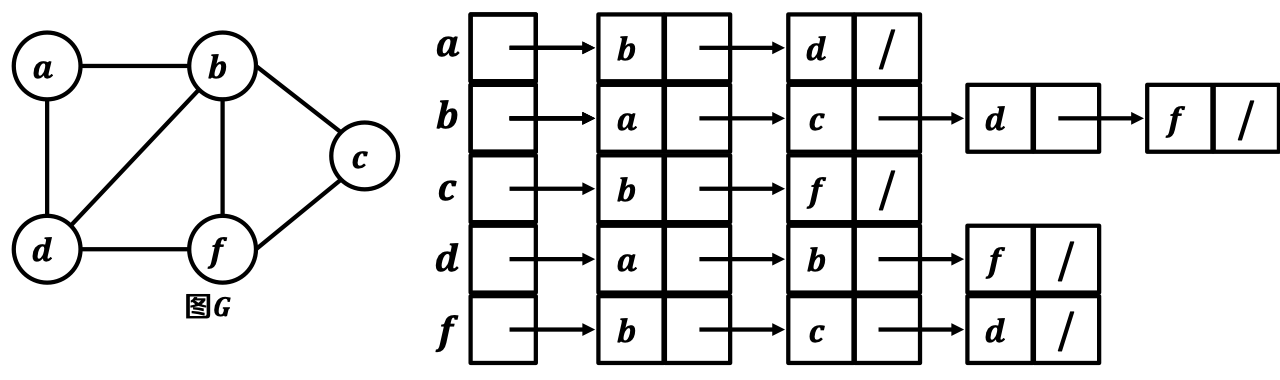
3.1. 邻接链表:
- 图𝑮 =< 𝑽, 𝑬 >,其邻接链表由条链表的数组构成;
- 每个顶点有一条链表,包含所有与其相邻的顶点;
- 空间大小𝑶();
- 利用握手定理解柯尼斯堡七桥问题:根据问题可知,从起点出发,经过图中所有边,最终到达终点:
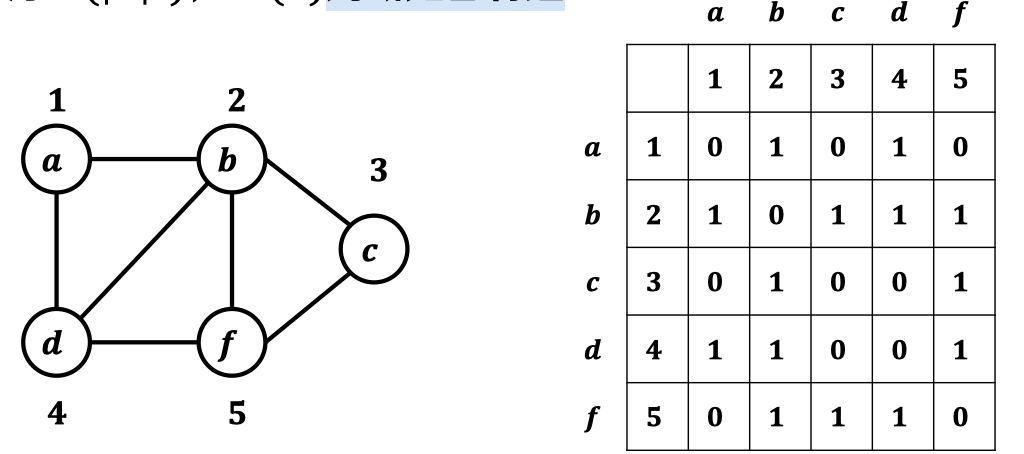
3.2. 邻接矩阵:
- 图𝑮 =< 𝑽, 𝑬 >的邻接矩阵由的二维数组构成;
- 空间大小为,判断节点间是否有边需要时间。