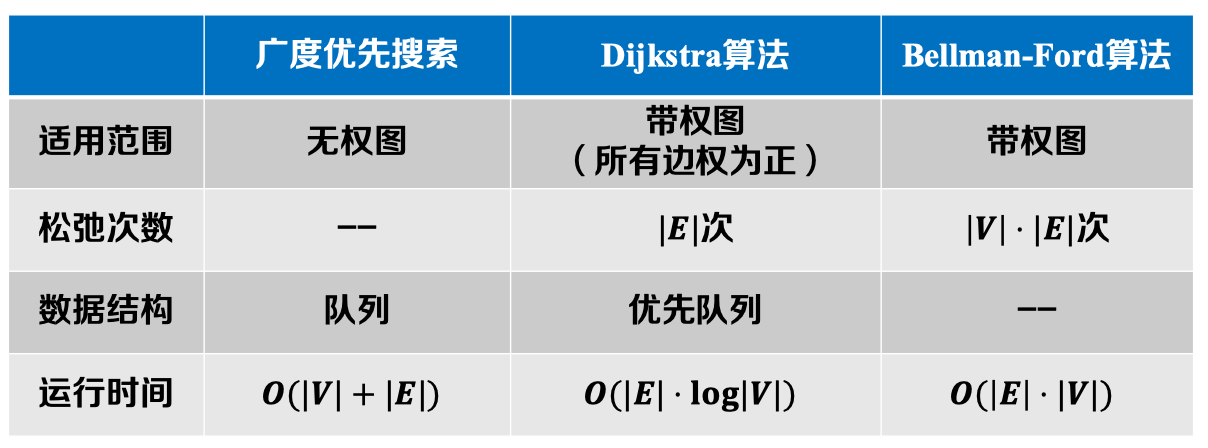
在前一篇文章中,主要介绍了如何利用Dijkstra算法解决正权图上的单源最短路径问题。然而,在现实生活中的许多图模型中,其权值并不一定全部为正。因此,本文将讨论带负权图上的单源最短路径问题。
本文概要:
- 算法背景
- 算法思想
- 算法实例
- 算法分析
- 算法性质
1. 算法背景——Dijkstra算法的局限性
考虑以下实例:
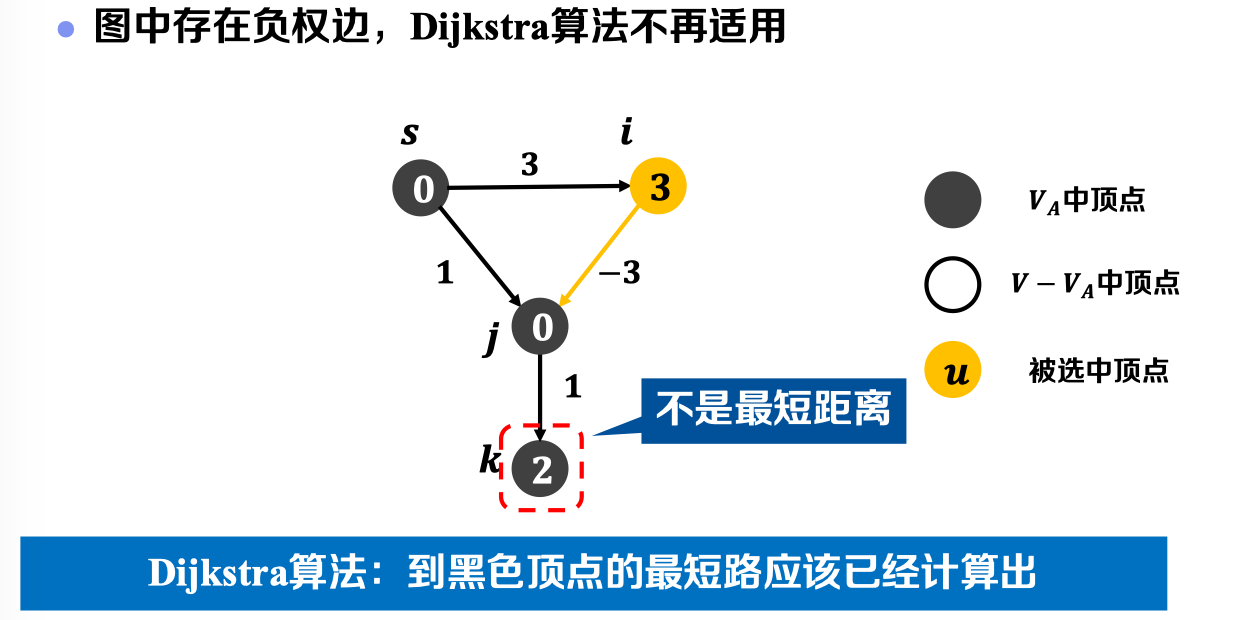
根据Dijkstra算法的思想,一旦确定源节点与任意节点最短距离后,在后续的过程中该距离将不会被松弛。然而,由于负权边的存在将与该情况发生冲突,因此Dijkstra算法无法适用于负权图上的单源最短路径问题。
根据上述情况随之需要思考:图中存在负权边时,是否一定存在单源最短路径?——不一定。考虑以下情况:
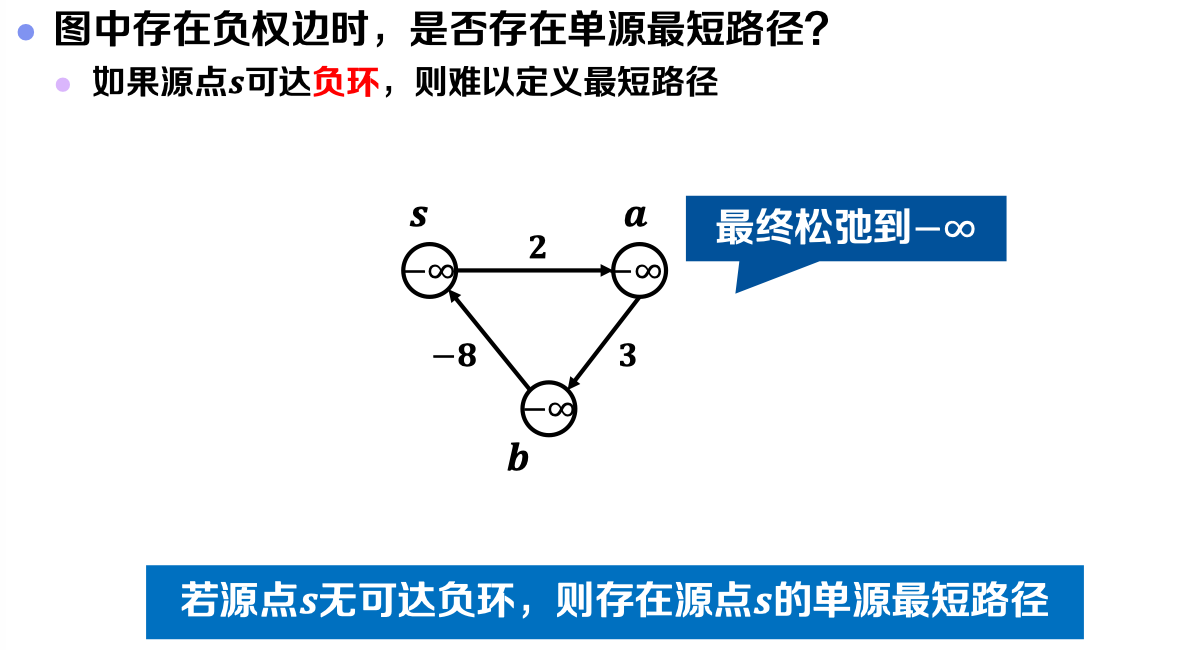
所以,若源点𝒔无可达负环,则存在源点𝒔的单源最短路径。
综上,我们给出图中允许出现负权边时的单源最短路径问题的定义:
定义. 单源最短路径问题(可含负权边):
- 输入:
- 带权图𝑮 =(𝑽, 𝑬, 𝑾 )
- 源点编号𝒔
- 输出:
- 源点𝒔到所有其他顶点𝒕的最短距离𝜹(𝒔, 𝒕)和最短路径< 𝒔, … , 𝒕 >
- 或存在源点𝒔可达的负环
根据问题定义可知,该问题存在以下两点挑战:
- 挑战𝟏:图中存在负权边时,如何求解单源最短路径?
- 挑战𝟐:图中存在负权边时,如何发现源点可达负环?
2. 算法思想——多轮松弛
在Dijkstra算法中,我们主要通过松弛操作迭代更新最短距离:

直观地,存在负权边时,需要比Dijkstra算法更多次数的松弛操作:
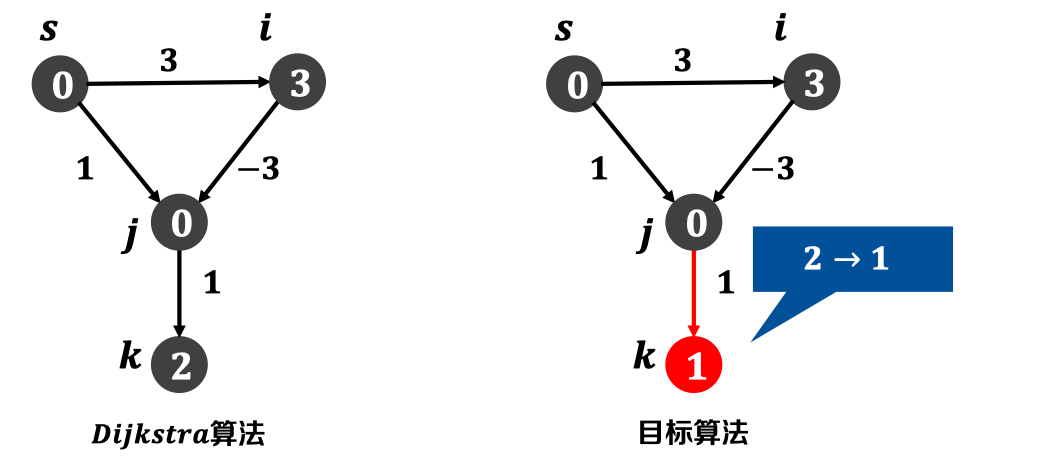
Bellman-Ford算法
- 解决挑战1:图中存在负权边时,如何求解单源最短路径?
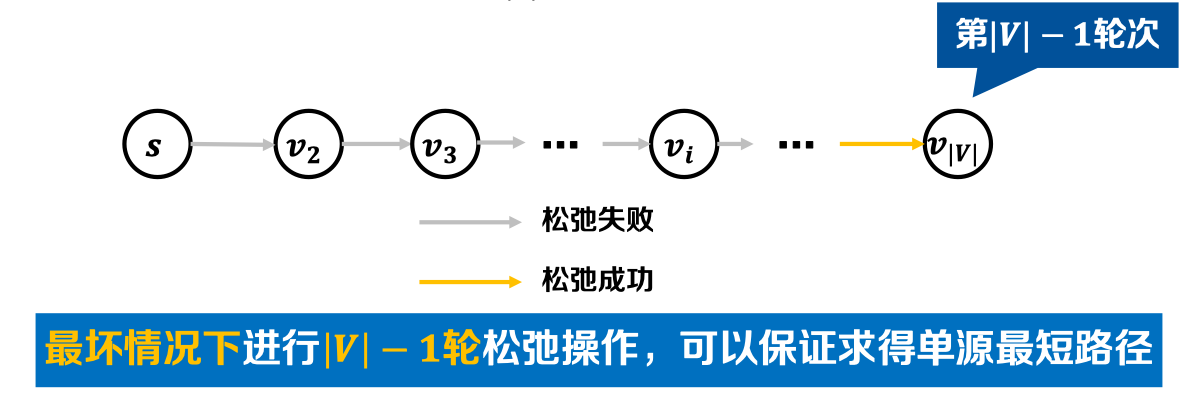
- 每轮对所有边进行松弛,持续迭代|𝑽 |-1轮
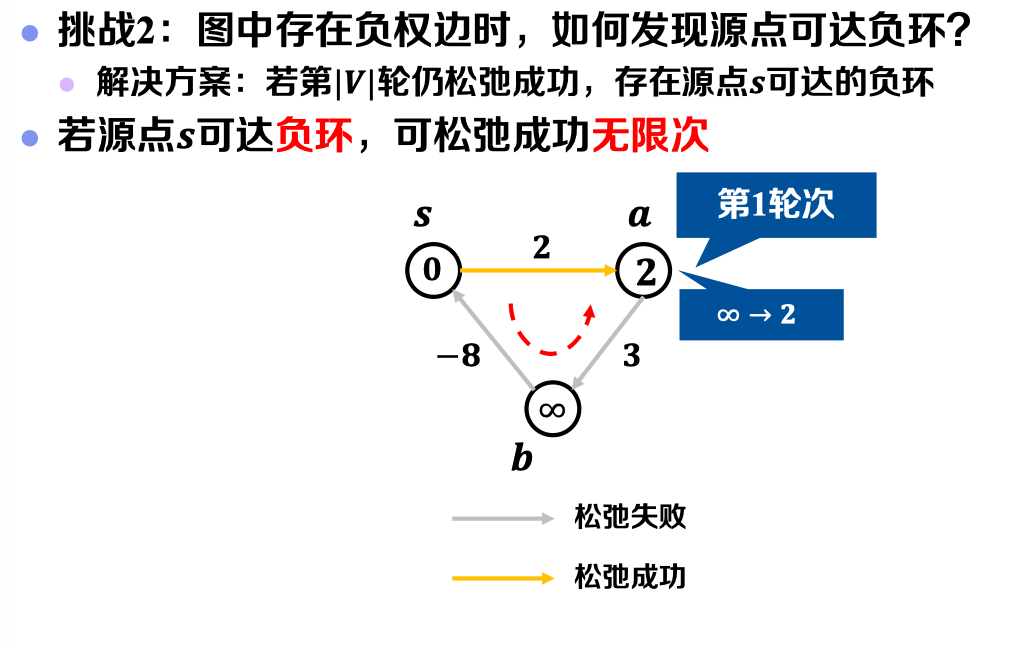
- 解决挑战2:图中存在负权边时,如何发现源点可达负环?
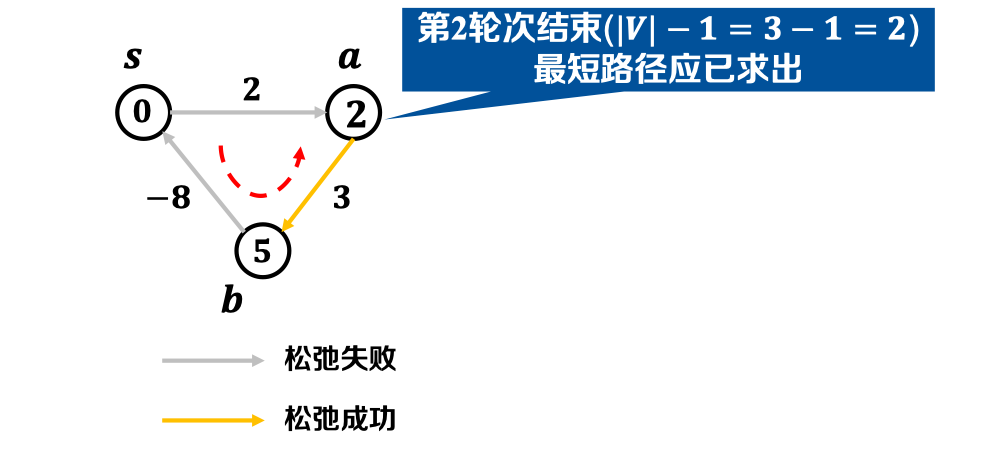
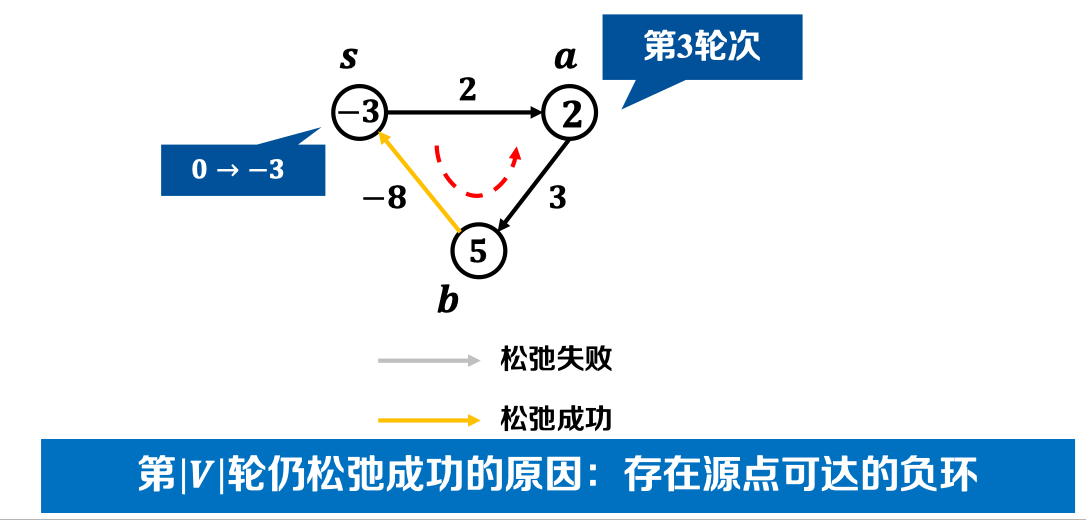
- 进行第|𝑽 |轮松弛,若仍松弛成功,存在源点𝒔可达的负环
3. 算法实例
初始时,我们任意给定一个松弛边的顺序:
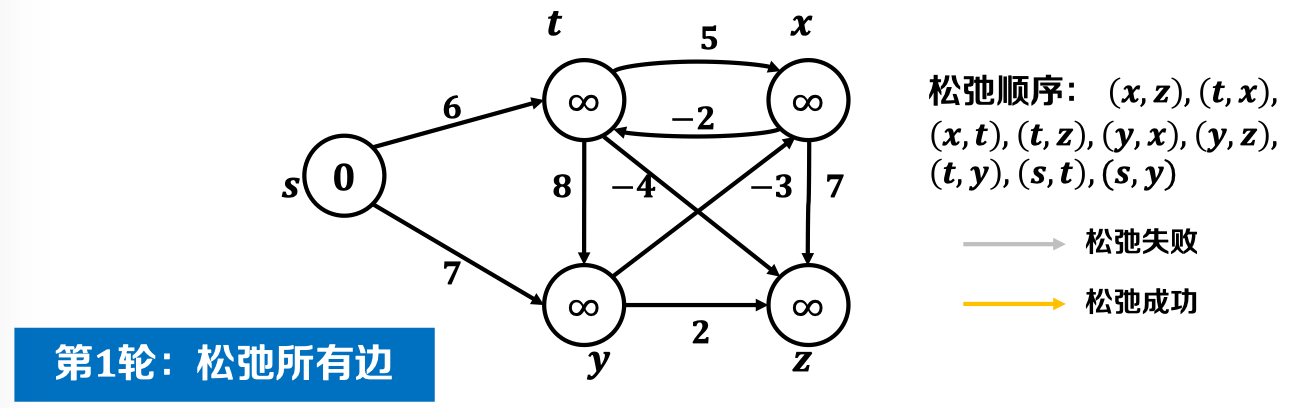
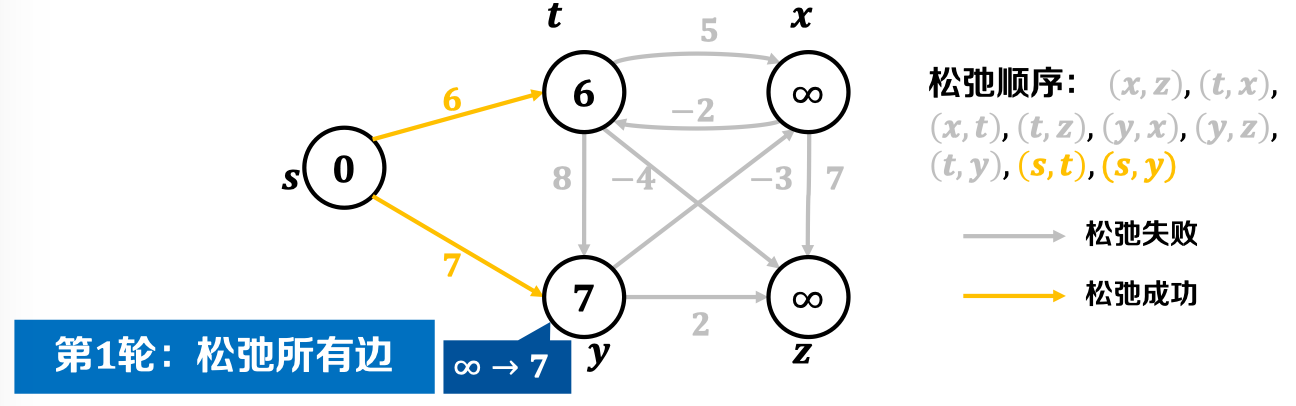
第一轮松弛后,结果如图:
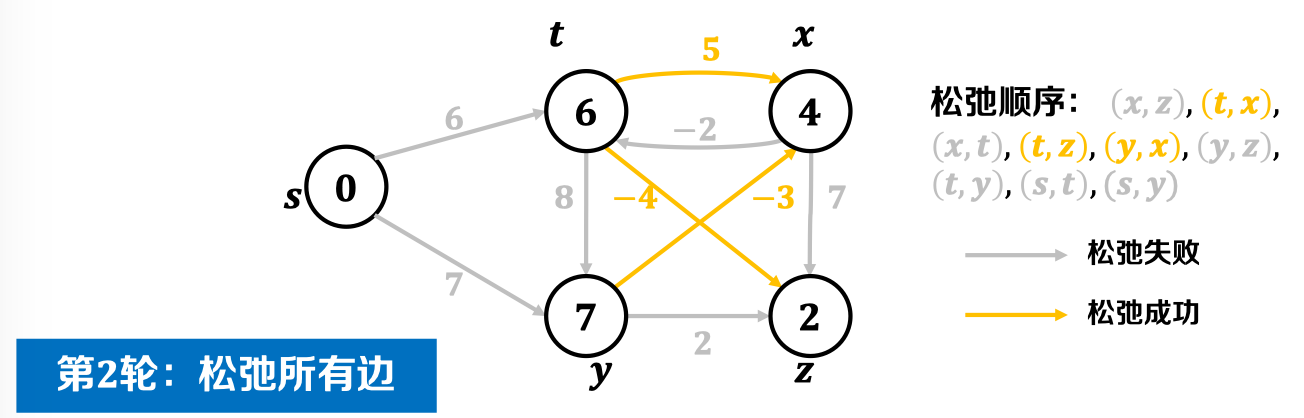
第二轮松弛后,结果如图:
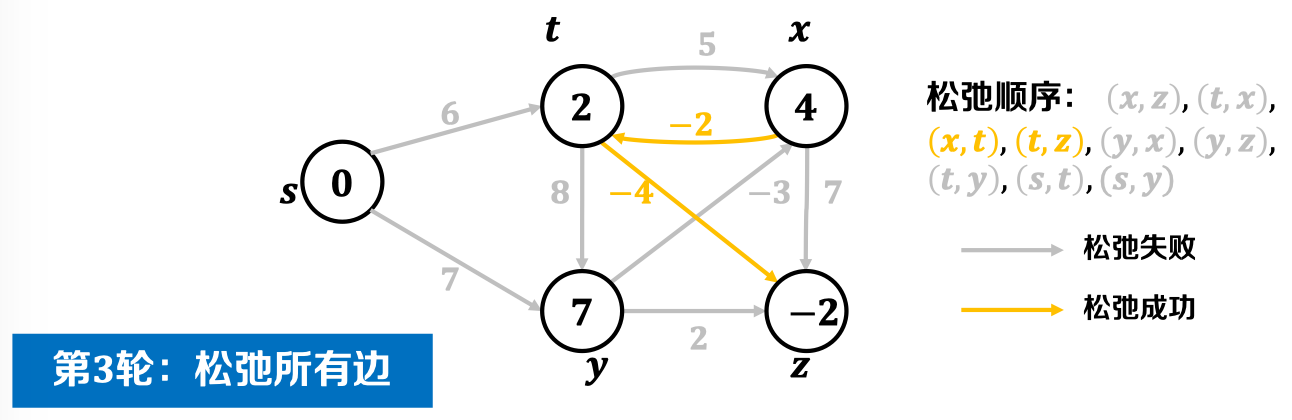
第三轮松弛后,结果如图:
第四轮松弛后,结果如图:
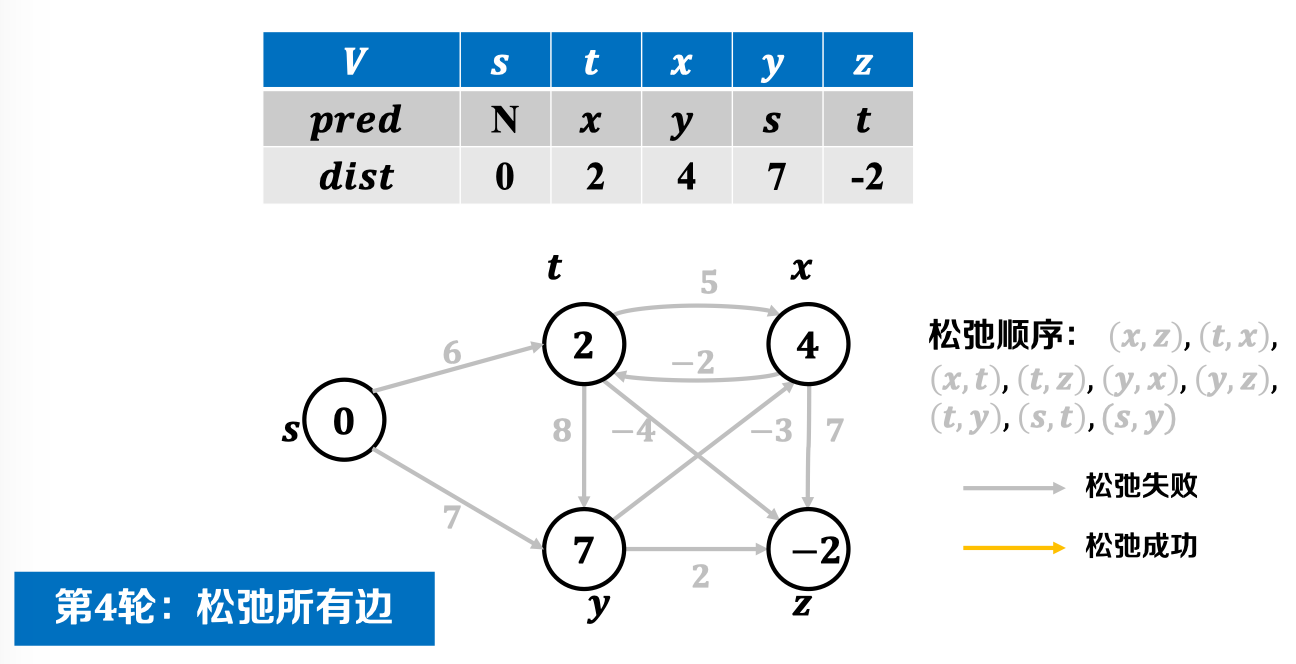
可见,第四轮后已经无法继续松弛,因此后续必然无法继续松弛,可得到最终结果。
4. 算法分析

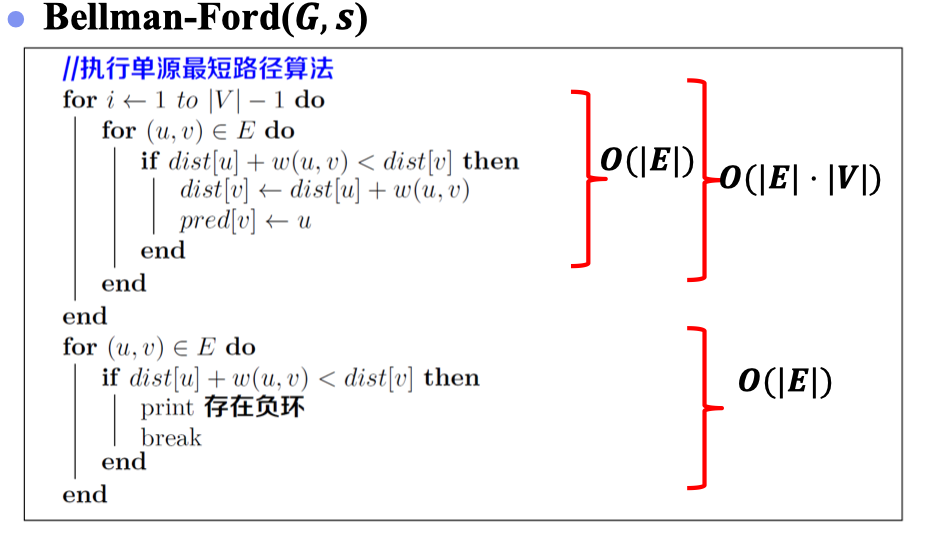
显然,该算法的复杂度为𝑶(|𝑬 | ⋅ |𝑽 |)
5. 算法性质——正确性证明:
- 挑战𝟏:图中存在负权边时,如何求解单源最短路径?——最坏情况分析
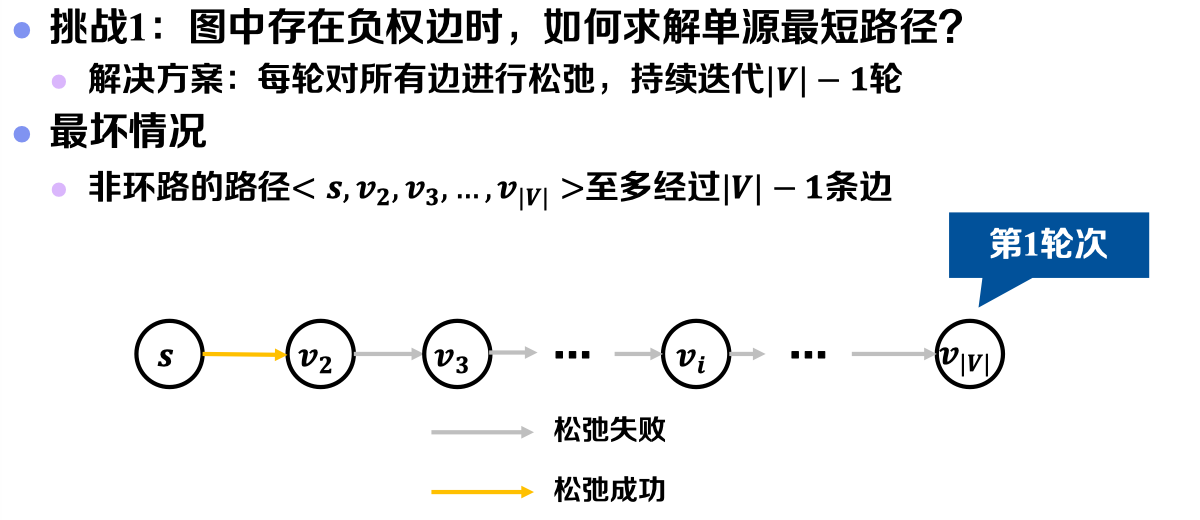
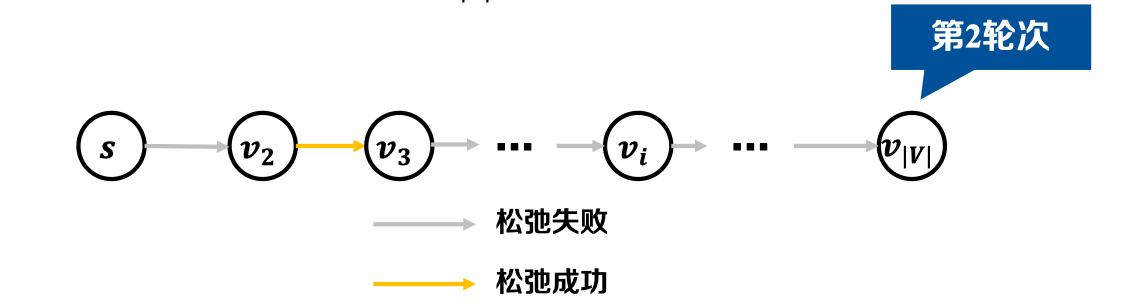
- 挑战𝟐:图中存在负权边时,如何发现源点可达负环?
6. 小结