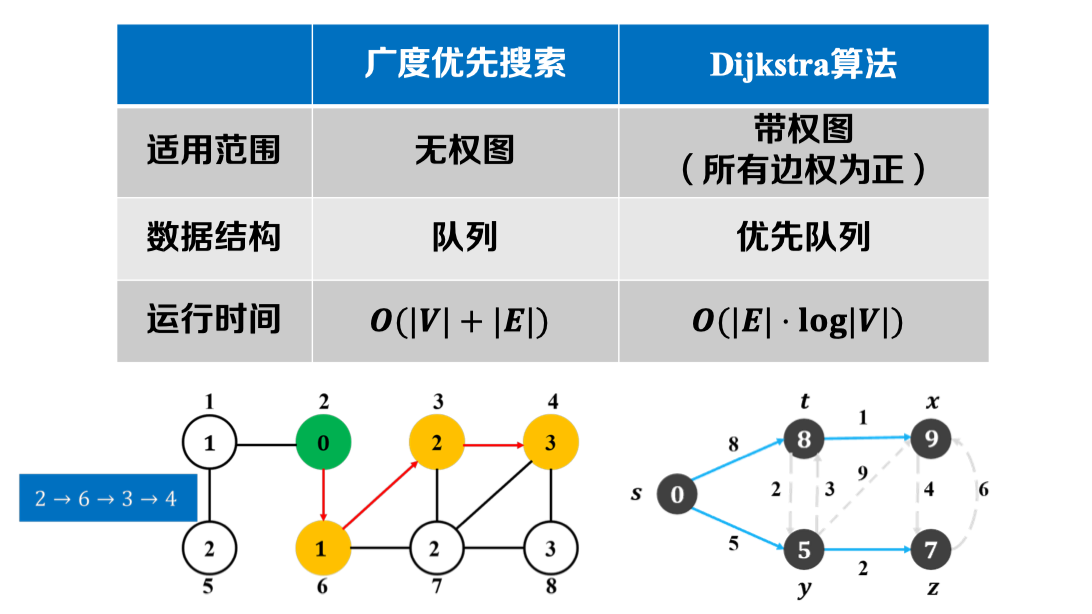
最短路径问题始终是图算法中一类重要的研究问题,目前也有众多工作提出了一些高效的解决策略。然而,就单源最短路径问题而言,Dijkstra算法和Bellman-Ford算法历经多年仍然是最经典的算法。本文将重点介绍Dijkstra算法。
本文概要:
- 算法背景
- 算法思想
- 算法实例
- 算法实现
- 算法分析
- 算法小结
1. 算法背景
最短路径问题的应用背景极其广泛,例如:查询从某地A到达目的地B的最短路径/时耗,查询社交网络中用户A和用户B之间最短的社交代价等等。其实,以上问题其实质均可建模为一类带权值的图模型。在本文中,我们重点讨论单源最短路径问题,即源节点确定的最短路径查询问题。回想一下,我们之前也说到:BFS搜素也可以解决一些最短路径,此处进行一些解释:
下图所示是一张地铁线路图,如果我们的问题是:需要求从地点A到地点B,如何规划路径可使得地铁经停最少车站。
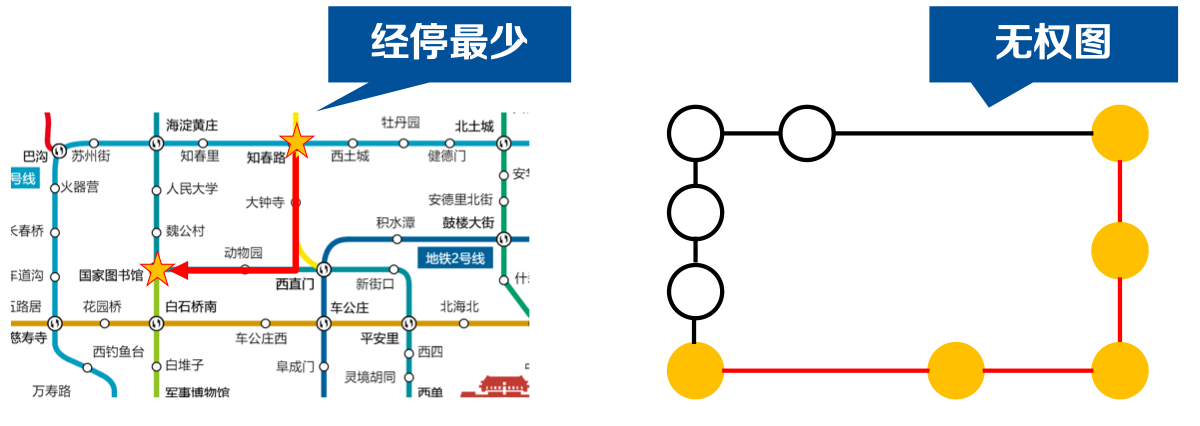
我们可以使用BFS算法即可求的相应结果,因为该问题其实可建模为在无权图(或所有边权值均为1的带权图)上的最短路问题。
然而,如果我们的问题是:需要求从地点A到地点B,如何规划路径可使得地铁运行时间最短。
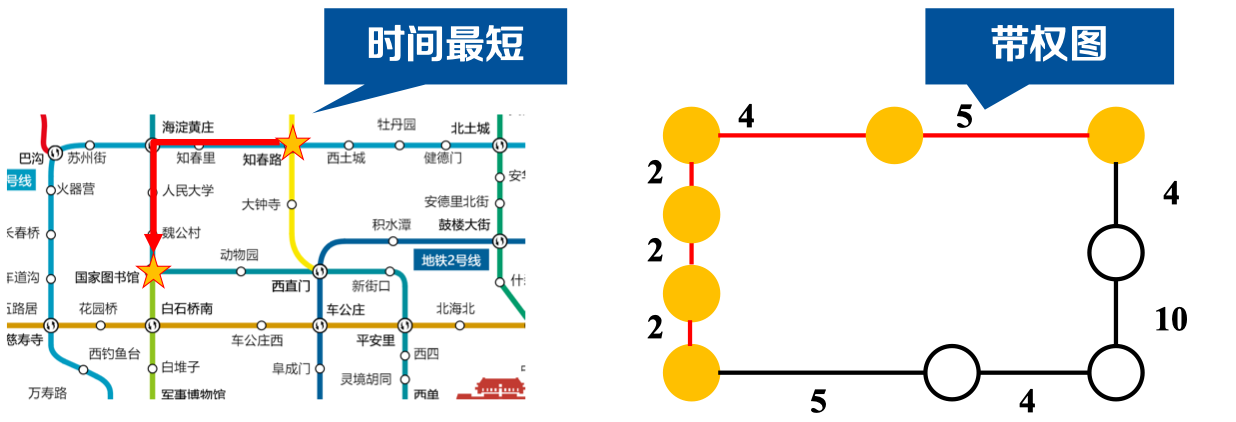
显然,该问题实质为如何计算带权图中源点到所有其他顶点的最短路径。对于带权图我们无法使用BFS方法直接求解,因此引出我们的Dijkstra算法。
我们首先给出问题的定义:
定义1.1 单源最短路径问题 (边权为正):
- 输入:
- 带权图𝑮 =(𝑽, 𝑬, 𝑾 ),其中𝒘(𝒖, 𝒗) ≥ 𝟎(图中所有边权为正), (𝒖, 𝒗) ∈ 𝑬
- 源点编号𝒔
- 输出:源点𝒔到所有其他顶点𝒕的最短距离𝜹(𝒔, 𝒕)和最短路径< 𝒔, … , 𝒕 >
P.s:需要强调的是,Dijkstra算法所能解决的是边权值权值均为正数的情况。对于权值为负数的情况,该算法并不能很好解决。
2. 算法思想
Dijkstra算法其算法思想与之前Prim算法求最小生成树有异曲同工之处,但由于其处理问题不同,故存在一定差异。
Dijkstra算法的实现我们同样借助辅助数组来完成:
- 𝒅𝒊𝒔𝒕表示距离上界(估计距离):
- 源点𝒔,𝒅𝒊𝒔𝒕[𝒔]= 𝟎;其他顶点𝒖,𝒅𝒊𝒔𝒕[𝒖]初始化为∞;
- 𝒅𝒊𝒔𝒕[𝒖]:源点𝒔到顶点𝒖的距离上界,𝜹(𝒔, 𝒖) ≤ 𝒅𝒊𝒔𝒕 𝒖
- 𝒄𝒐𝒍𝒐𝒓表示顶点状态:
- 黑色:到顶点𝒖最短路已被确定
- 白色:到顶点𝒖最短路尚未被确定
- 𝒑𝒓𝒆𝒅表示前驱顶点:
- (𝒑𝒓𝒆𝒅[𝒖] , 𝒖)𝒊为最短路径上的边
总结算法的核心思想如下:
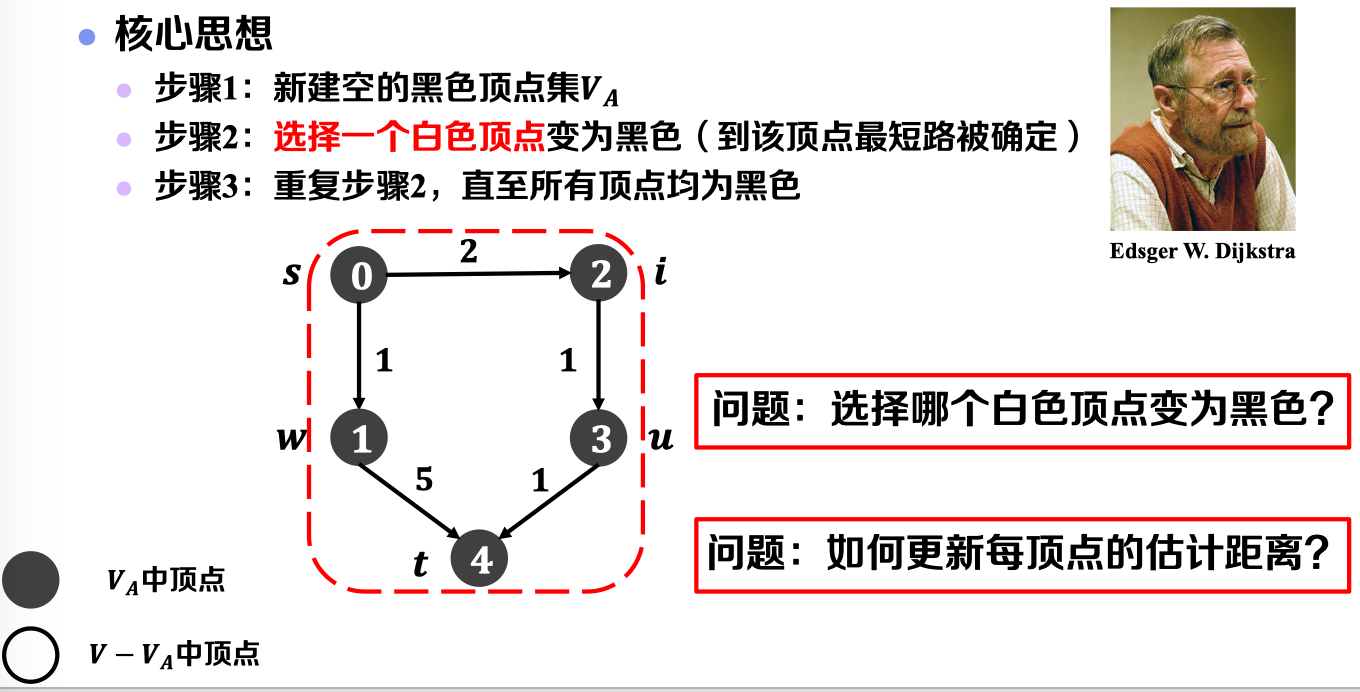
目前存在以下两个问题:
- 选择哪个白色顶点变为黑色——贪心策略选择
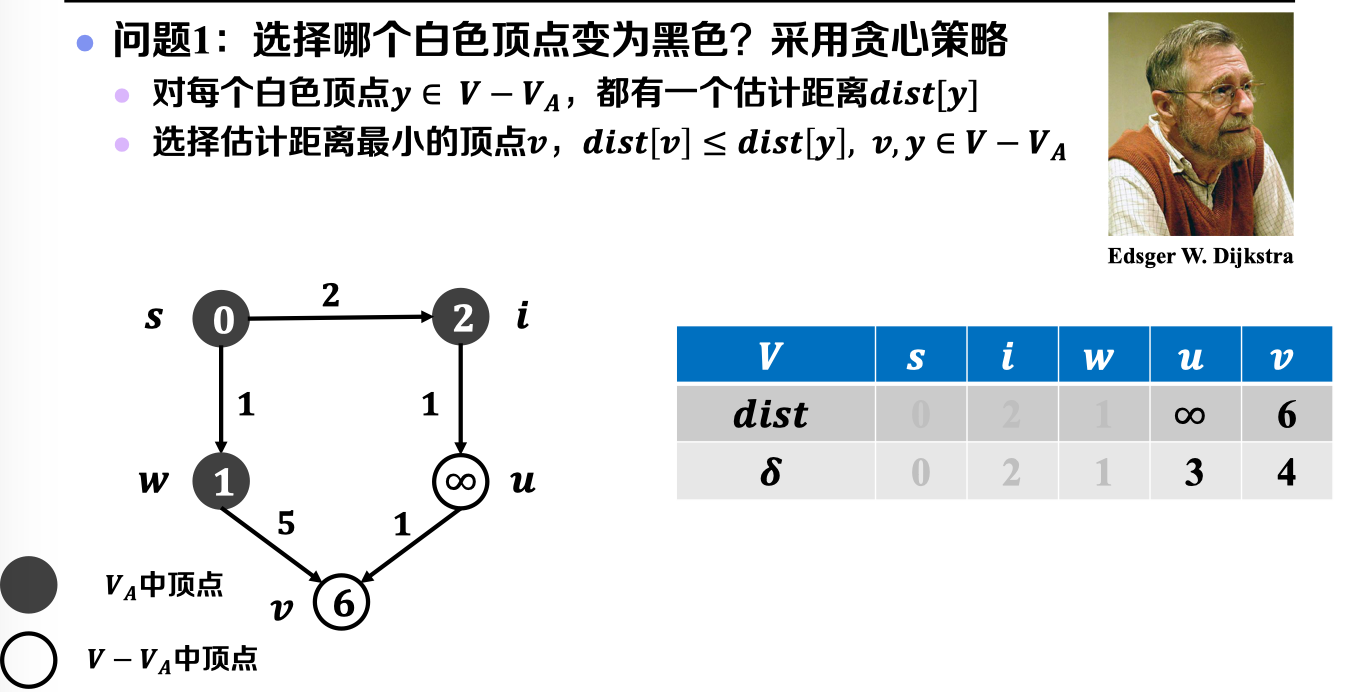
- 如何更新每顶点的估计距离——利用已选节点进行松弛处理
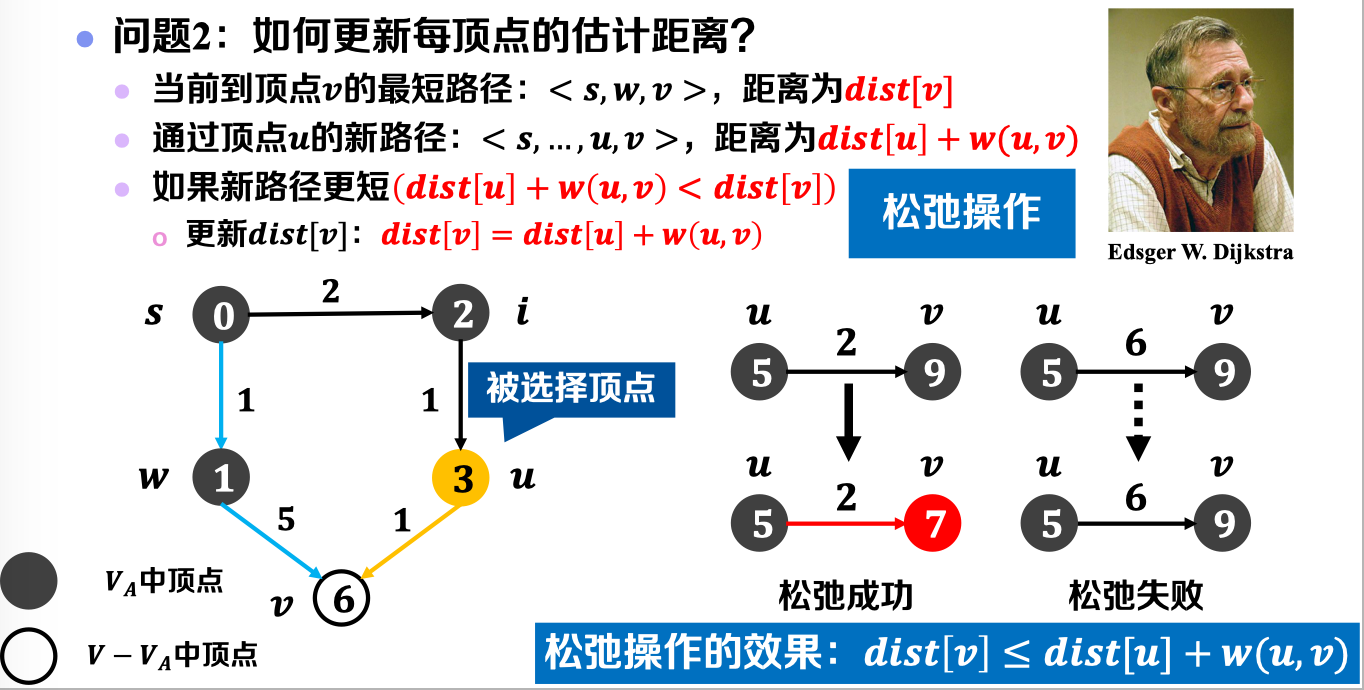
3. 算法实例
初始时:
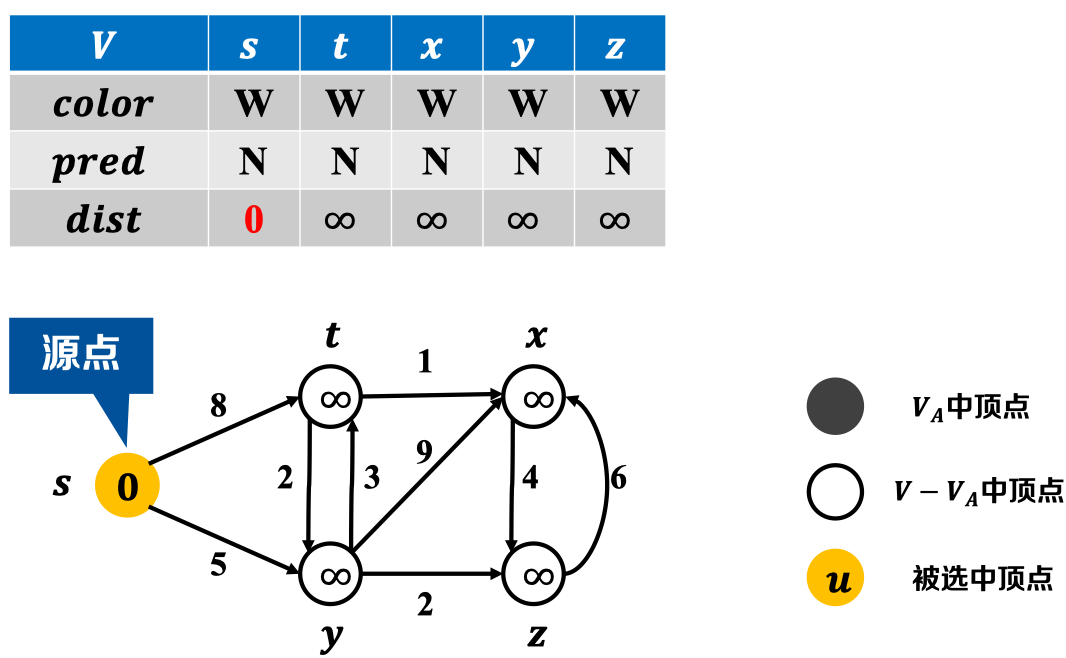
利用当前已确定节点松弛其相邻接节点:
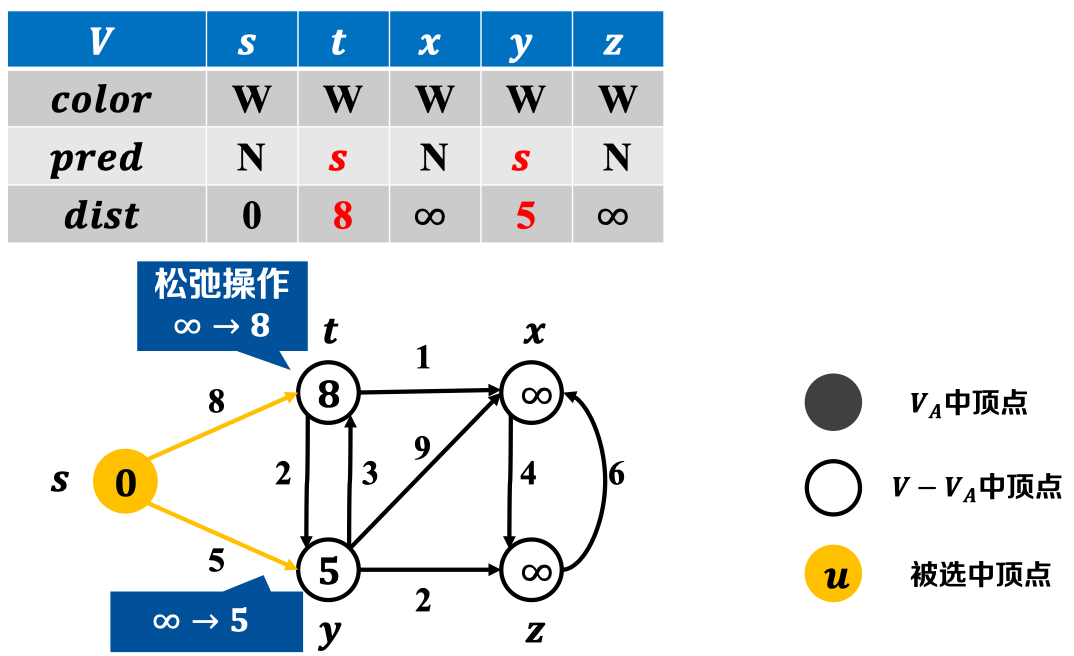
之后,贪心选择当前估计距离最小的节点:
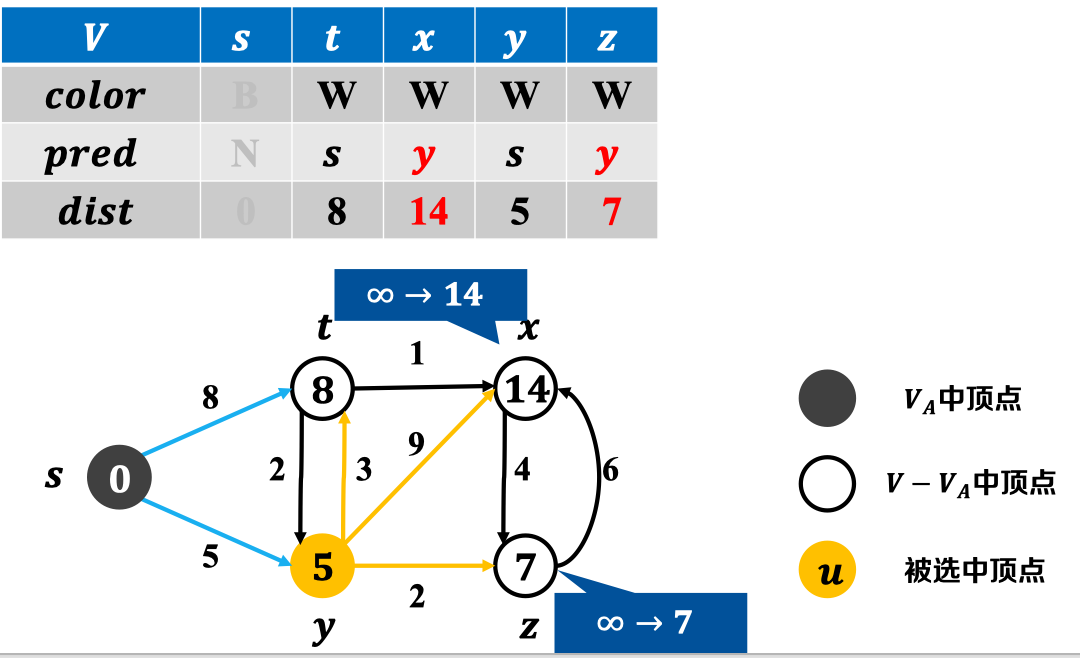
重复上述过程,直至确定源节点到所有节点的最小距离:
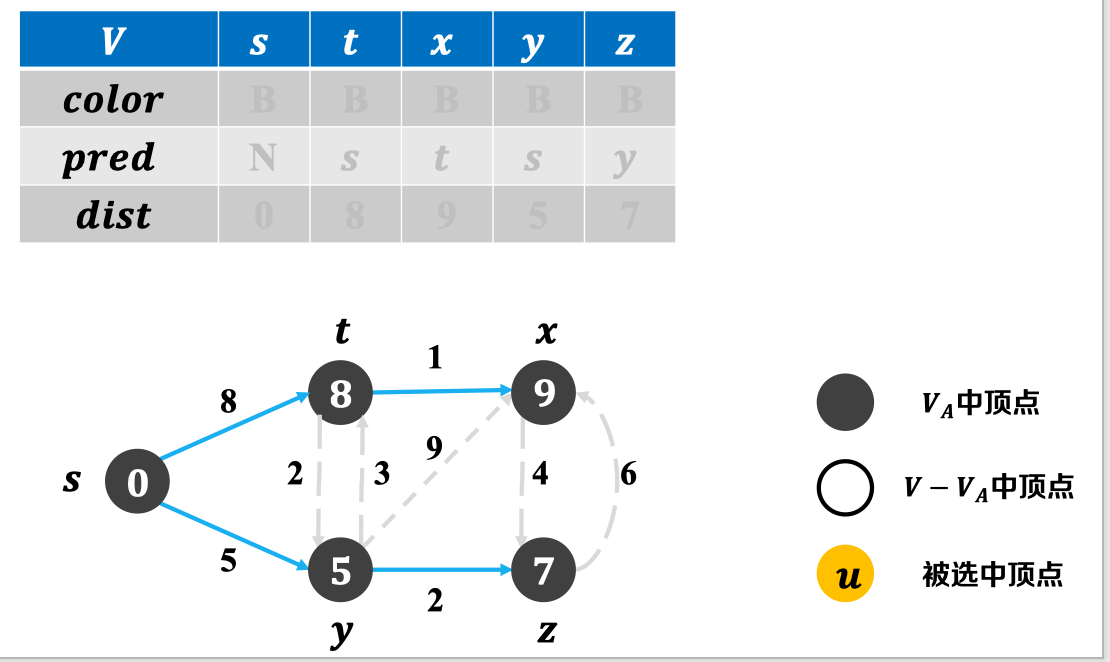
4. 算法实现
通过上述实例演示,其实我们不难发现:Dijkstra算法整个算法流程与Prim算法的实现很类似。以下我们给出Dijkstra算法直观实现的伪代码:

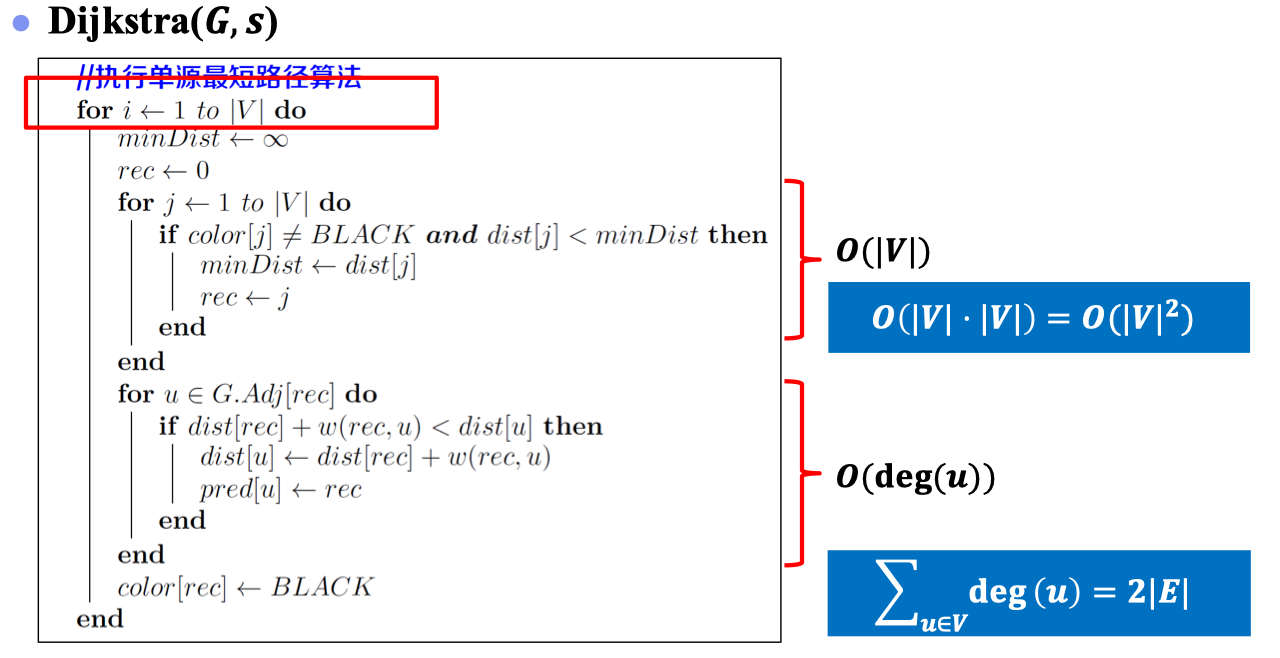
以上对于Dijkstra算法朴素地实现,其复杂度为。
显然,算法中贪心选择𝒅𝒊𝒔𝒕数组中最小的节点仍然可以借助优先队列实现,以此来降低算法复杂度:


可见,通过优先队列实现Dijkstra算法,可将复杂度降至。
5.算法分析
童咏昕老师在《算法设计与分析》课程中详细讲解了Dijkstra算法的正确性证明:


该证明使用反证法,巧妙地借助了逆否命题与原命题等价证得Dijkstra算法的正确性。反证法也是证明算法正确性时常用的方法之一。
6.算法小结
6.1 Dijkstra算法 & Prim算法
Dijkstra算法与Prim算法有很多相似之处:
- 均是基于贪心策略的算法;
- 均使用𝒅𝒊𝒔𝒕数组;
- 算法过程中,均需要不断更新𝒅𝒊𝒔𝒕数组;
但同时,Dijkstra算法与Prim算法由于其处理问题不同,故仍存在差异:
- 虽然均需要使用𝒅𝒊𝒔𝒕数组,但𝒅𝒊𝒔𝒕数组作用不同:
- Prim算法中,𝒅𝒊𝒔𝒕数组用于记录横跨割的边的权重;
- Dijkstra算法中,𝒅𝒊𝒔𝒕数组用于记录距离上界(估计距离);
- P.s:Prim算法需要维护候选轻边权重;Dijkstra算法需要维护源节点到任意节点间路径最短距离。
- 更新𝒅𝒊𝒔𝒕数组的方法不同:
- Prim算法将一个节点选入子树后,判断该节点到邻居节点的距离是否小于𝒅𝒊𝒔𝒕[v];
- Dijkstra算法确定源节点到一个节点的最短距离后,判断利用源节点到节点的最短路径能否将源节点到节点的邻居节点的距离松弛,即:𝒅𝒊𝒔𝒕[u]+$w(u,v)\leq $𝒅𝒊𝒔𝒕[v];
6.2 Dijkstra算法 & BFS算法