之前，我们介绍了单源最短路径问题：Dijkstra算法——解决正权边图上的单源最短路径；Bellman-Ford算法——解决图上带负权边的单源最短路径问题。而今天，我们将主要介绍一种解决图上多元最短路径的算法——Floyd算法。

本文概要：

  • 算法背景
  • 算法思想
  • 算法实例
  • 算法实现

P.s：本文图例参考：原文链接

1. 算法背景

现实生活中，我们的需求时常不仅仅是求得某地到其他各地的最短距离，更常见的情况是我们需要知道各地之间的最短距离。一种朴素且可行的想法是：对于图中每个节点使用解决单源最短路径问题的算法（Dijkstra算法 或 Bellman-Ford算法）。然而，在现实环境中图数据规模庞大，该方法的时间复杂度显然是我们所难以接受的。因此，我们需要一种高效的方法解决这样一个多源最短路径问题。

解决多源最短路径问题的众多算法中，最为人们所熟知的是Floyd算法。该算法凭借其明了的思想、简洁的代码实现，被大家称之为一个短小精悍的算法。本文将在后续部分主要介绍该算法的核心思想。

2. 算法思想

之前在介绍Dijkstra算法时，我们首次提出了**“松弛”**的思想，并强调这一思想是大多数最短路算法的核心思想。因此，Floyd算法也不例外，其核心思想概括而言是——动态规划策略+松弛。
在正式介绍算法之前，我们对下图进行观察：

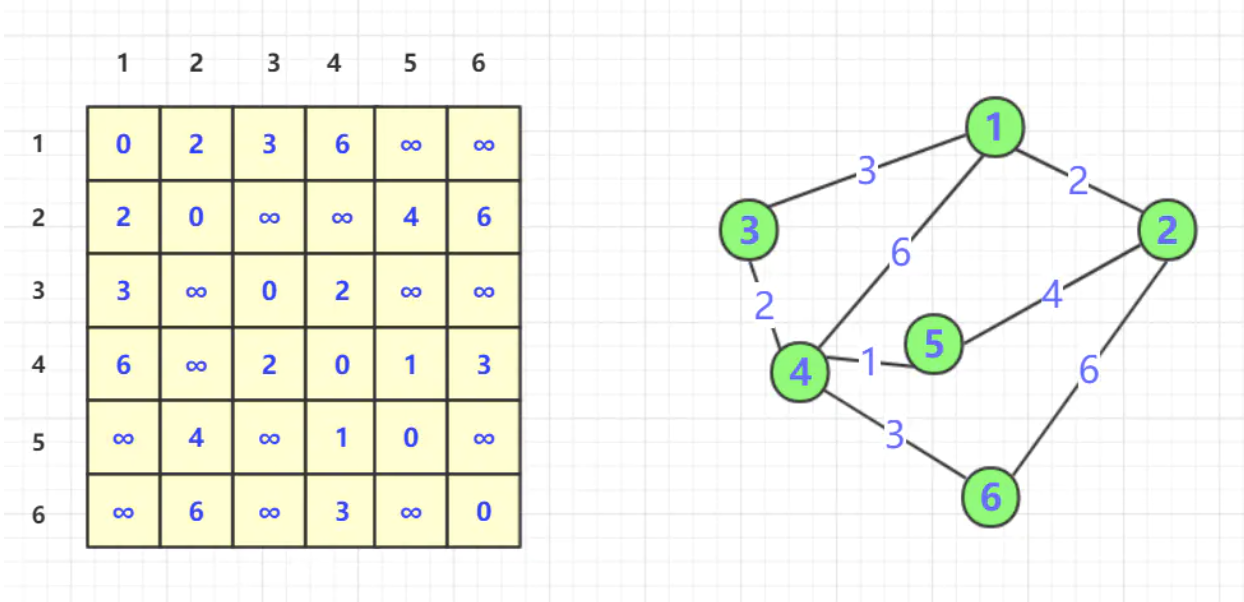
不难发现，在不考虑其他节点/路径的情况下，节点1→41\to 4之间的最短距离即为边(1,4)(1,4)的权值6。然而，如果我们引入节点33，并利用边(1,3),(3,4)(1,3),(3,4)可将节点1→41\to 4之间的最短距离更新为55，即松弛成功。
因此，我们不难想到——对图中所有点均进行试探，判断每一个点对间的距离是否因为加入的点而更新，即可得到任意两点间的最短距离。这便是Floyd算法的核心思想。总结如下：
1）利用邻接矩阵dist[i][j]储存节点i,ji,j间的最短距离。如果没有直接相连的两点那么默认为一个很大的值，并且其到自己的长度为0；
2）从第1个到第∣V∣|V|个点依次加入图中。每个点加入进行试探是否有路径长度被更新；
3）上述试探具体方法为遍历图中每一个点(i,j双重循环)，判断每一个点对距离是否因为加入的点而发生最小距离变化。如果发生改变，那么两点(i,j)距离就更新；
4）重复上述直到最后插点试探完成。

3. 算法实例

依然沿用我们上述的图例：

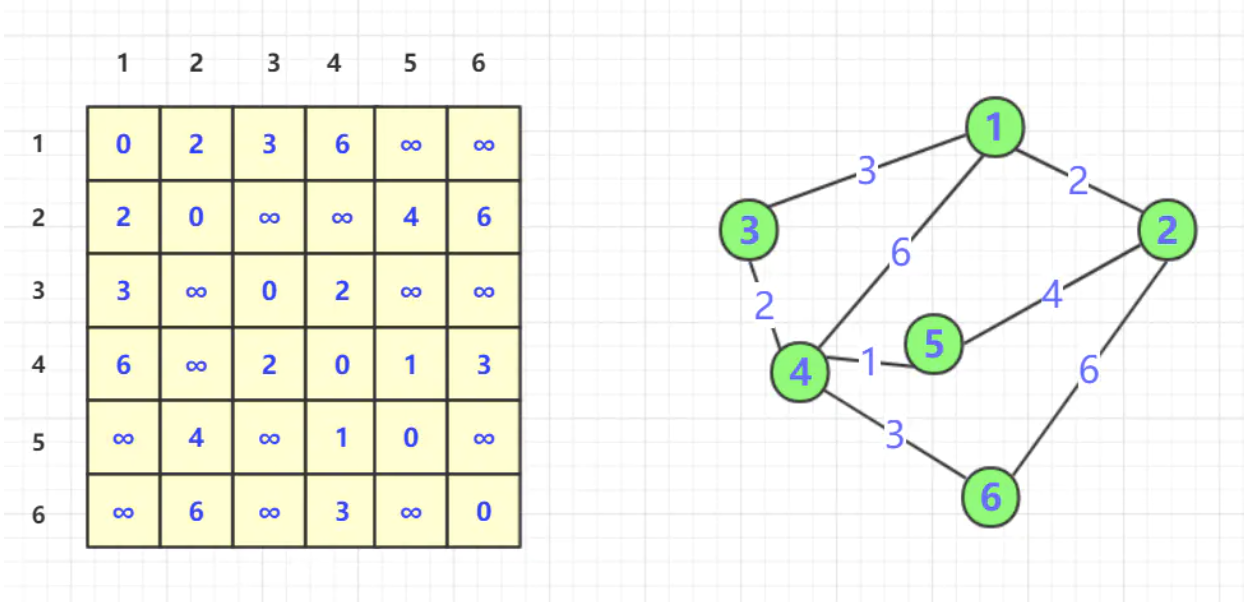
利用邻接矩阵dist[i][j]储存节点i,ji,j间的最短距离，上述dist[i][j]矩阵展示了初始阶段的内容。之后我们对图中每个节点进行试探：

对于节点1进行试探：由于1的加入，使得本来不连通的2，3点对和2，4点对变得联通，并且加入1后距离为当前最小。同时，我们发现加入1其中也使得产生路径3$\to11\to4，但是路径34，但是路径3\to11\to$4的距离为9远远大于本来的(3,4)为2，所以不进行更新。

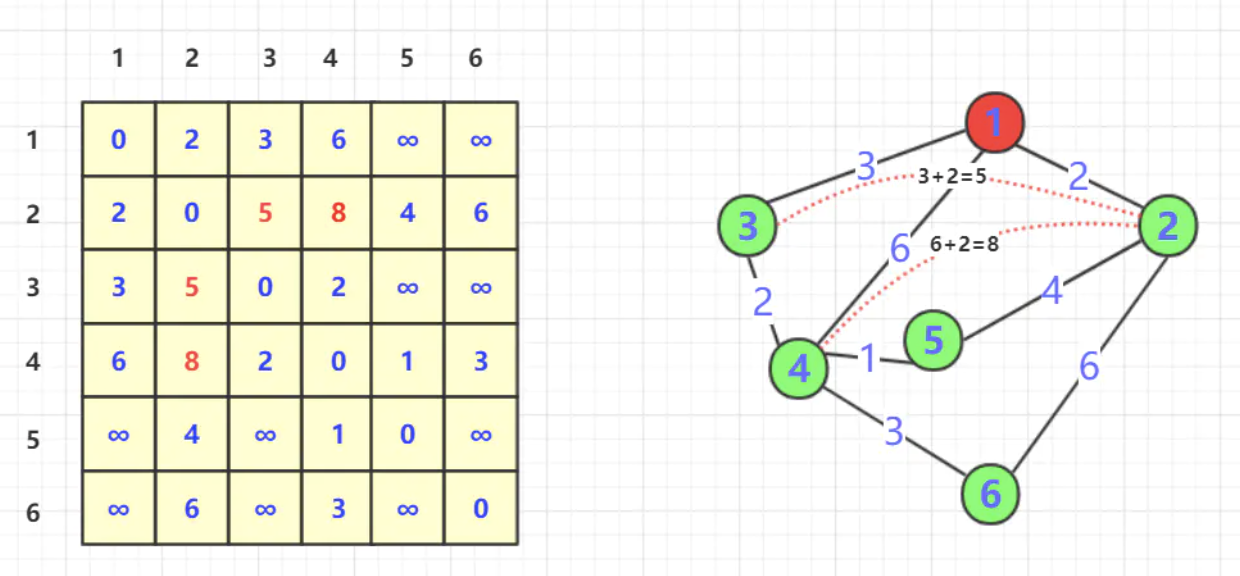
对于节点2进行试探：

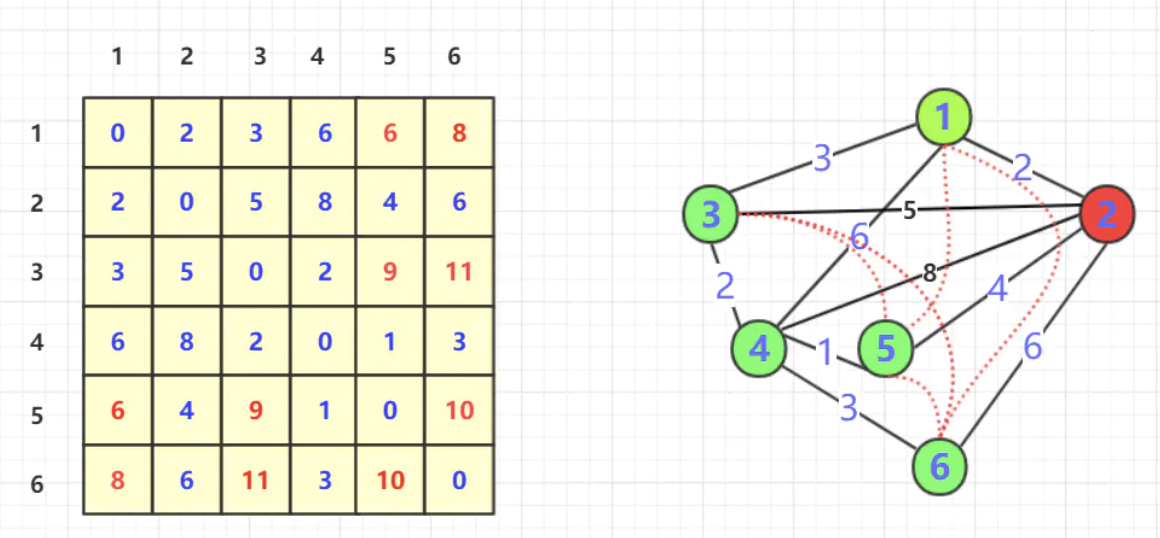
后续同理。

4. 算法实现

Floyd算法的实现非常简洁，其核心代码仅需要三层循环即可：

for(int i = 1; i <= n; i++)
{
    for(int j = 1; j <= n; j++)
    {
        for(int k = 1; k <= n; k++)
        {
            if(dis[j][k] > dis[j][i] + dis[i][k])
            {
                dis[j][k] = dis[j][i] + dis[i][k];
            }
        }
    }
}

显然，该算法复杂度为O(∣V∣3)O(|V|^3)。