图算法：图搜索算法——广度优先搜索（BFS）& 深度优先搜索（DFS）

本文主要介绍两类最基本的图搜索策略——BFS与DFS。BFS与DFS是一种最基础的，但也是最重要的图算法，其被大量应用在图算法的各个领域，众多高级的图算法，其核心其实仍是这两种最基础的图搜索算法。
本文主要依据北京航空航天大学童咏昕教授《算法设计与分析》课程内容，并结合本人对于图数据的研究课题内容，对图搜索上的两类基础算法进行总结。
P.s：本文主要关注无向图上的BFS与DFS算法，关于有向图的搜索算法会在后续进行讨论。

本文内容概要：

图搜索应用及背景
广度优先搜索（BFS）
深度优先搜索（DFS）

1. 图搜索

每当提及图搜索问题，便不得不提及图上的可达性查询问题，即：给定图 $G$ 与查询节点 $u$ , $v$ ，我们需要回答图上是否存在一条路径使得查询节点 $u,v$ 之间可达。可达性查询问题是图查询问题中一类最基本，也是最重要的问题，是大多数查询问题的基础。可达性查询问题在现实生活中也具有大量的应用场景，如：社交网络查询任意用户之间的好友关系查询、任意两地之间道路交通的可达性查询等。
近年来，大量的科研工作已在可达性查询问题上进行了深入且细致的研究，提出了包括链分解、树覆盖、区间标记、2-Hop在内的多种高效的查询方法。此外，其研究对象也从传统的静态图进一步讨论到动态图、时间依赖图以至于演化图流序列等。
然而，无论目前在可达性查询领域有多少先进的查询方法，其最基本的思路均集中在如何构建规模合理的查询索引以提升查询效率。换言之，目前的方法均采用以空间成本换取时间成本的策略。关于可达性查询问题上时空代价的权衡可参见下图：

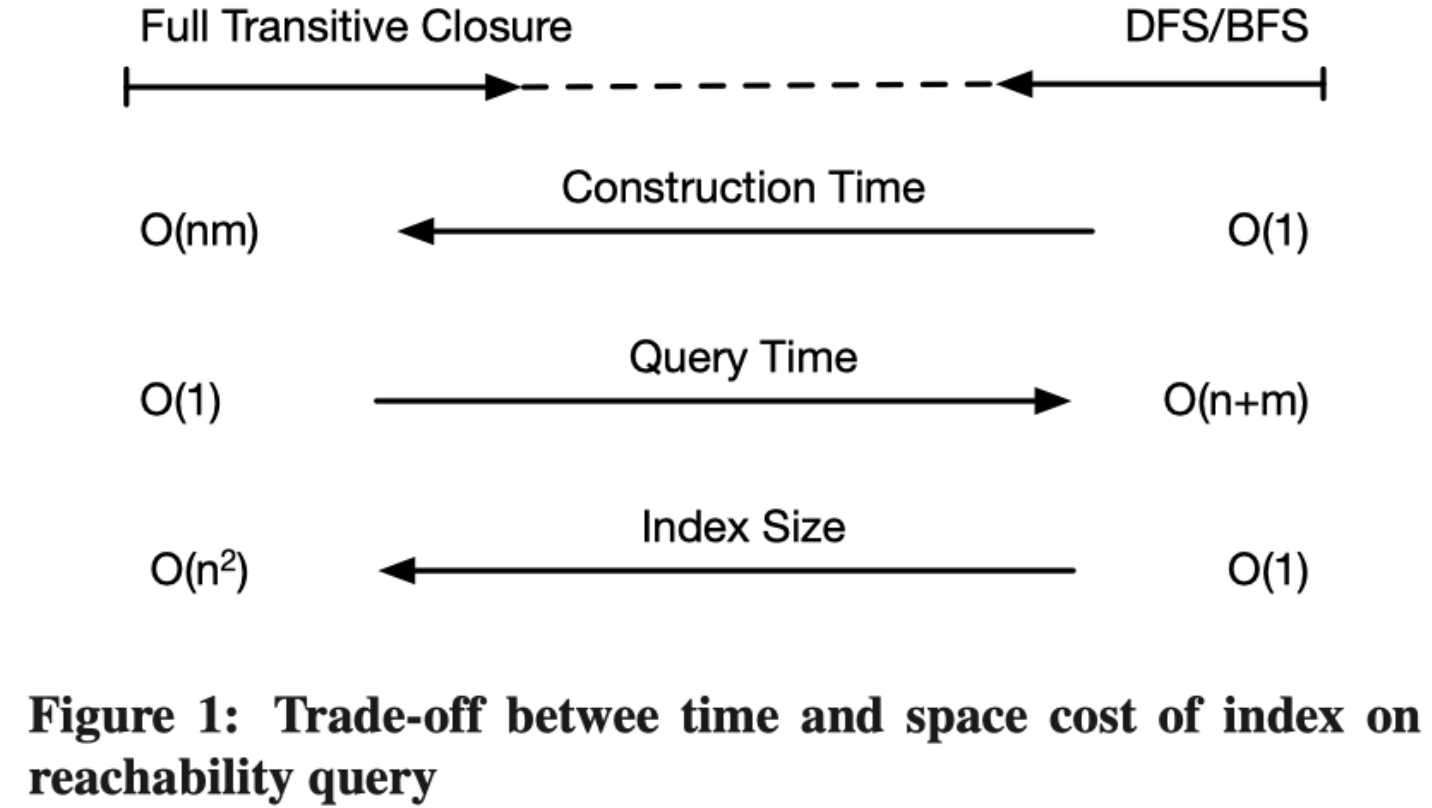
在本文中，我们并不对当前最新进的图搜索方法进行介绍，而是对最基础的两类图搜索算法进行介绍。只有切实掌握了最基础的方法，才能进一步掌握更高效的方法。

2. 广度优先搜索（BFS）

2.1 算法思想：

童咏昕教授在《算法设计与分析》课程中介绍的思想很形象地诠释了BFS的核心思——水滴落入水面所激起的涟漪会向相邻区域逐渐扩散。如下图所示：

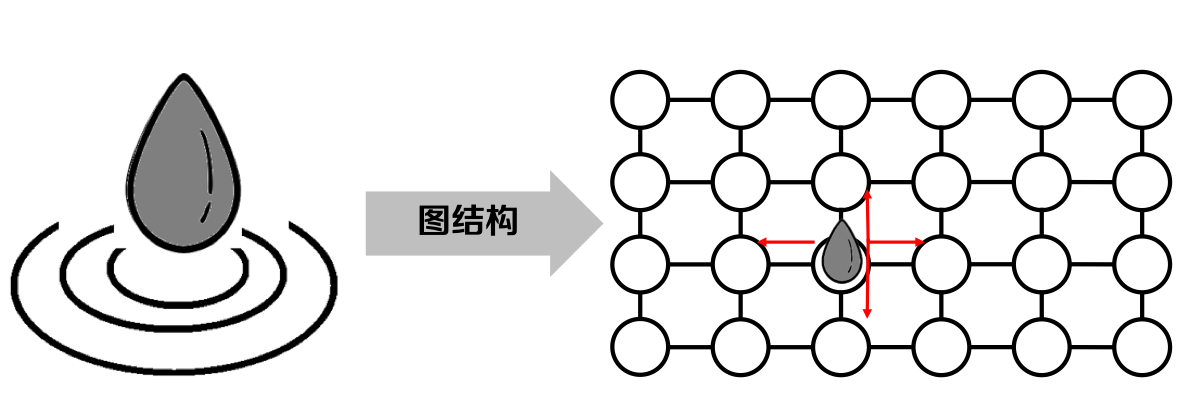
这种依次扩散的现象，蕴含了搜索图结构的一种顺序，即：处理某顶点时，一次性发现所有其相邻顶点。其实质可以称之为一种“分层”搜索的思想。该方法在多处同时“扩散”时，为了维护节点处理顺序需要借助“队列”这常用的数据结构。（p.s：队列的性质为先进先出（First In First Out，FIFO））。
综上所述，BFS的核心思想：处理某顶点时，一次性发现其所有相邻顶点，未处理顶点加入等待队列。

2.2 算法实现：

BFS算法的实现多种多样，可以根据自己的具体应用需求设计相应实现方法。本文中采用《算法设计与分析》课程中提出的实现方法，该方法更易于理解BFS的核心思想，也有助于后续对BFS的应用。
算法首先需要借助以下三类辅助数组维护相关节点信息：

𝒄𝒐𝒍𝒐𝒓数组表示顶点状态：
- 𝑾𝒉𝒊𝒕𝒆：白色顶点——𝒖尚未被发现，发现后直接入队；
- 𝑩𝒍𝒂𝒄𝒌：黑色顶点——𝒖已被处理，无需再次入队；
- 𝑮𝒓𝒂𝒚：灰色顶点——𝒖已加入队列，无需再次入队。
𝒑𝒓𝒆𝒅数组：表明顶点uu的前驱节点，即：节点uu由𝒑𝒓𝒆𝒅[u]发现
𝒅𝒊𝒔𝒕数组：顶点uu距离源点的距离。

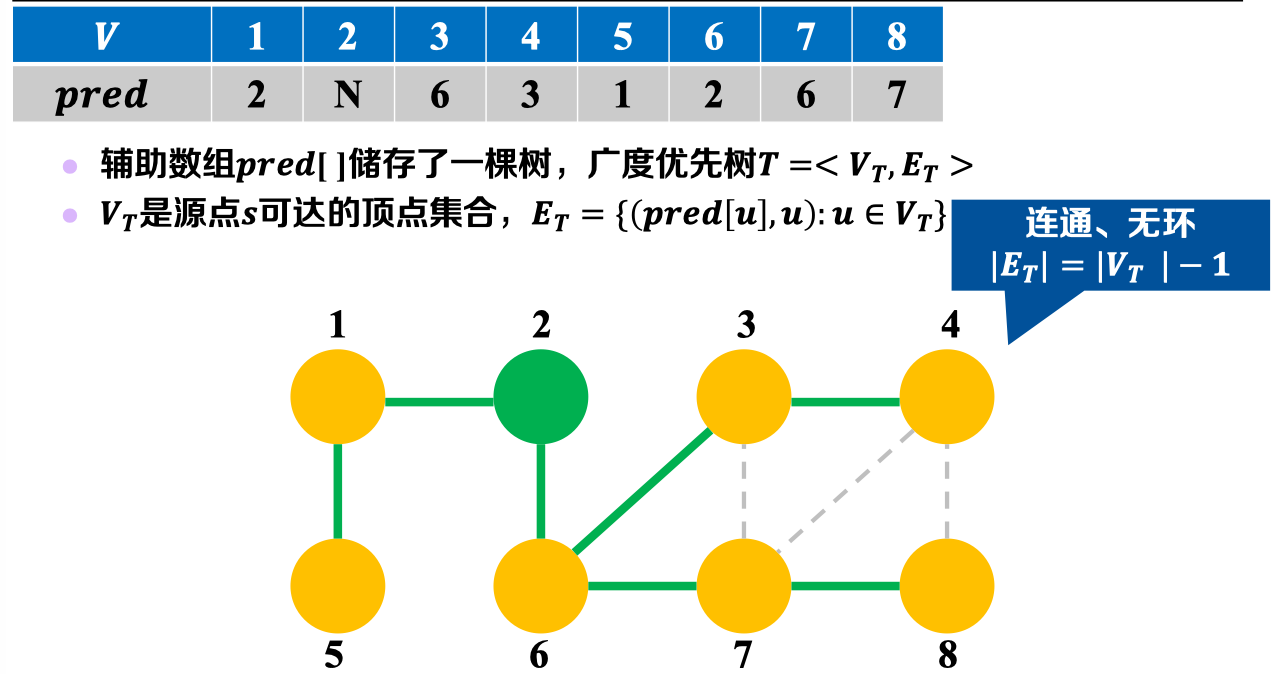
实例演示：

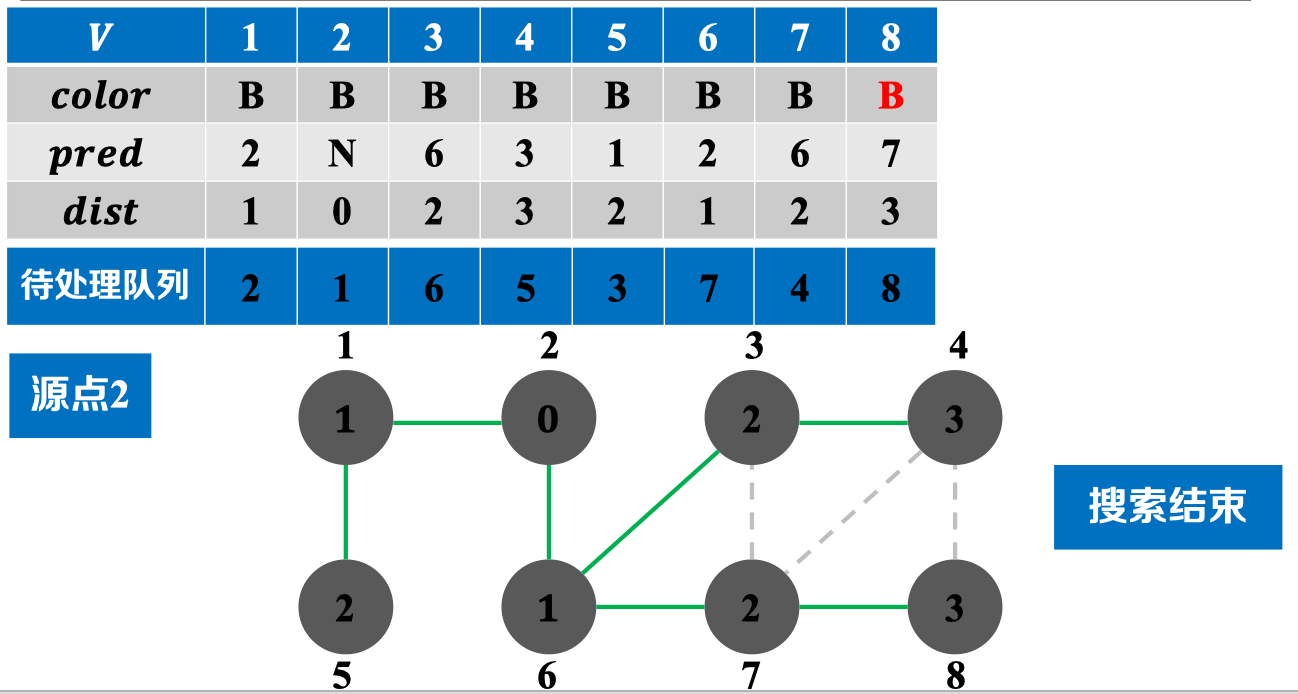
P.s: 需要注意的是，由BFS算法中的𝒑𝒓𝒆𝒅数组可衍生出广度优先树：

2.3 算法伪代码：

2.4 算法复杂度分析：

对于每个顶点 $u$ ，搜索其相邻顶点消耗时间 $𝑻_𝒖= 𝑶(𝟏) + 𝒅𝒆𝒈(𝒖)$
总运行时间： $𝑻 < \sum_{u\in V} 𝑻_𝒖$ $T < \sum_{u \in V} T_{u}$
- 可推得： $\sum_{u\in V} 𝑻_𝒖=\sum_{u\in V} 𝑶(𝟏 + 𝒅𝒆𝒈(𝒖))=\sum_{u\in V} 𝑶(𝟏)+\sum_{u\in V} 𝑶(𝒅𝒆𝒈(𝒖))=𝑶(|V|)+\sum_{u\in V} 𝑶(𝒅𝒆𝒈(𝒖))$
- 由握手定理可知：𝒅𝒆𝒈(G)=2|E|；
综上所述： $𝑻=𝑶(|V|+|E|)$

2.5 其他应用：

结合BFS中构建的𝒑𝒓𝒆𝒅数组与𝒅𝒊𝒔𝒕数组，我们可以得到源节点到达其可达节点的最短距离：

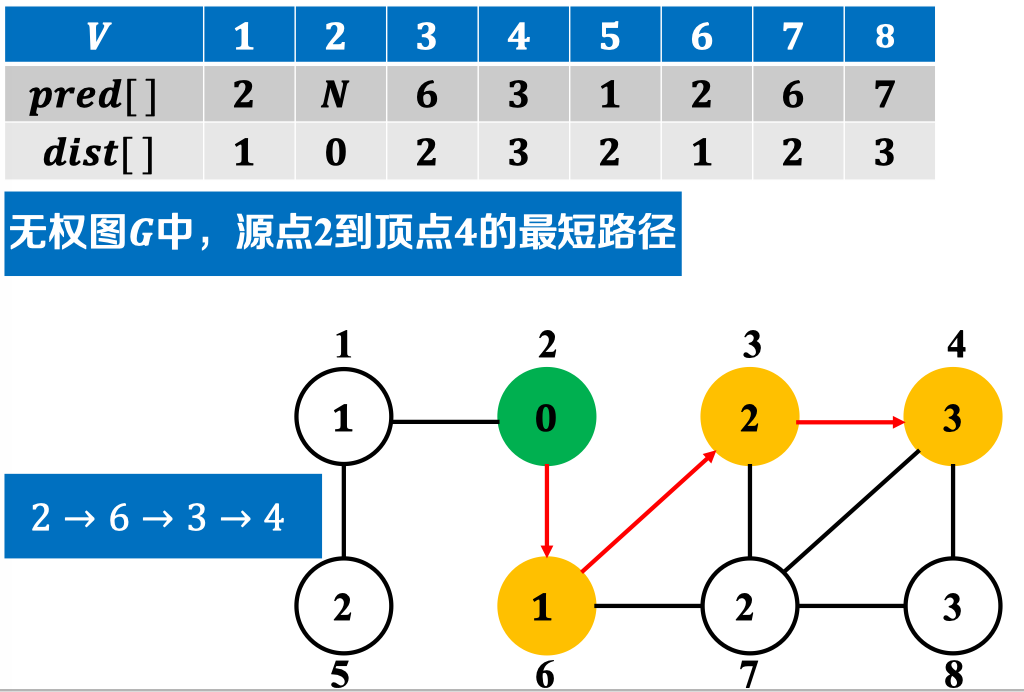
该方法使后续最短距离算法的核心与基础

3.深度优先搜索（DFS）

3.1 算法思想：

深度优先搜索其核心是基于一种回溯的思想，即：“一条路走到黑”的搜索策略。详细而言，其算法步骤可分为以下三步：

分叉时，任选一条边深入；
无边时，后退一步找新边；
找到边，从新边继续深入。

3.2 算法实现：

与BFS策略相同，DFS算法的实现也多种多样，此处的实现策略主要为了便于体现算法思想以及后续性质介绍。在具体项目中，需要根据项目需求自行调整实现过程。
与BFS的实现类似，我们同样借助辅助数组来实现DFS算法：
P.s：此处使用多个辅助数组来进行实现，虽然显得较为繁复，但每个数组在后续DFS应用中均有重要作用。

𝒄𝒐𝒍𝒐𝒓数组表示顶点状态：
- 𝑾𝒉𝒊𝒕𝒆：白色顶点——𝒖尚未被发现；
- 𝑩𝒍𝒂𝒄𝒌：黑色顶点——𝒖已被处理；
- 𝑮𝒓𝒂𝒚：灰色顶点——𝒖正在处理。
𝒑𝒓𝒆𝒅数组：表明顶点u的前驱节点，即：节点u由𝒑𝒓𝒆𝒅[u]发现
𝒅数组：顶点发现时刻（变成灰色的时刻）
𝒇数组：顶点完成时刻（变成黑色的时刻）

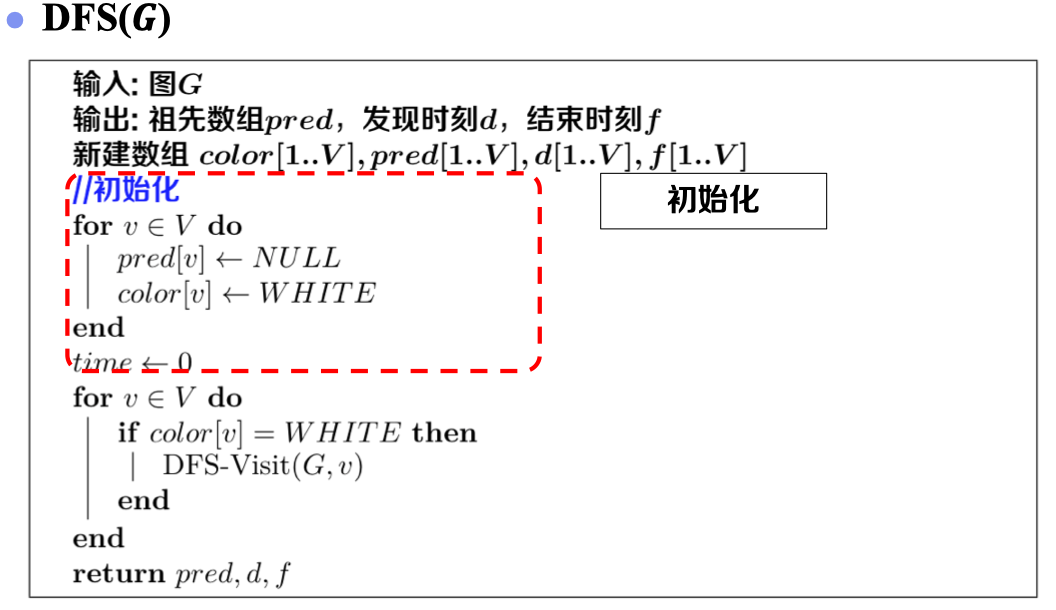
3.3 算法伪代码：

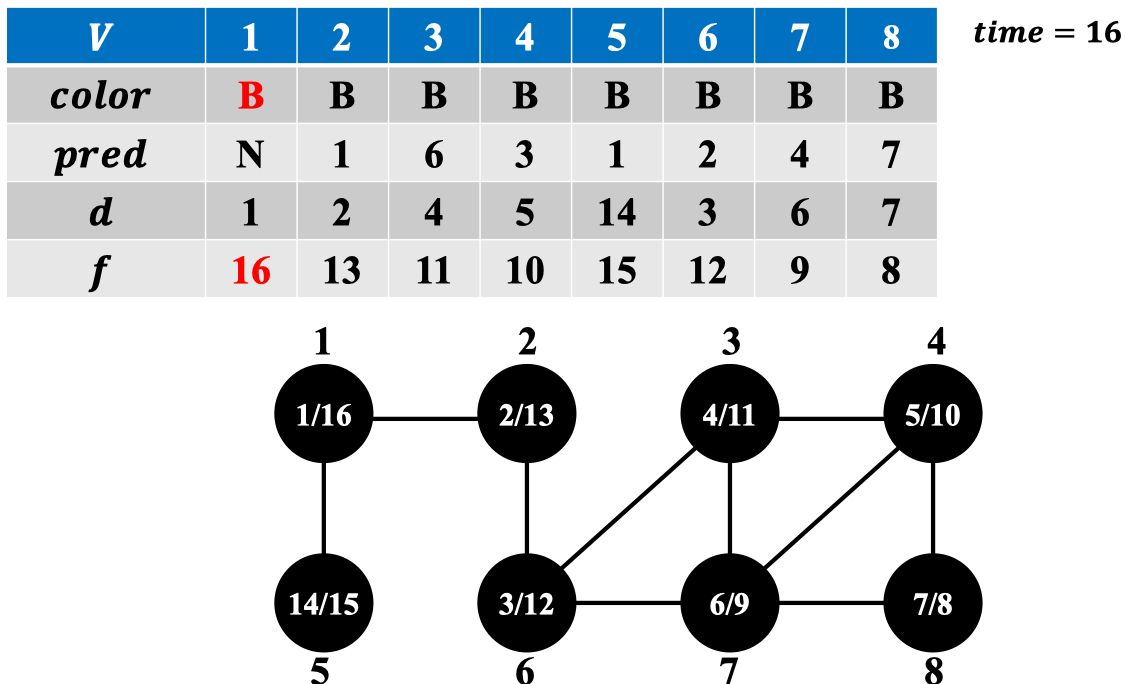
3.4 实例演示：

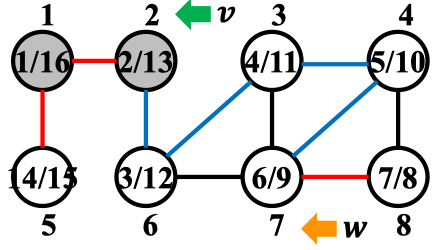
我们以1号节点作为源节点执行DFS算法：

3.5 复杂性分析：

值得注意的是，虽然DFS涉及递归调用，但是其子问题个数、子问题规模均难以确定。因此，难以使用主定理法或递归树法进行分析。我们仍对DFS过程中，任意一个顶点v的开销进行分析：

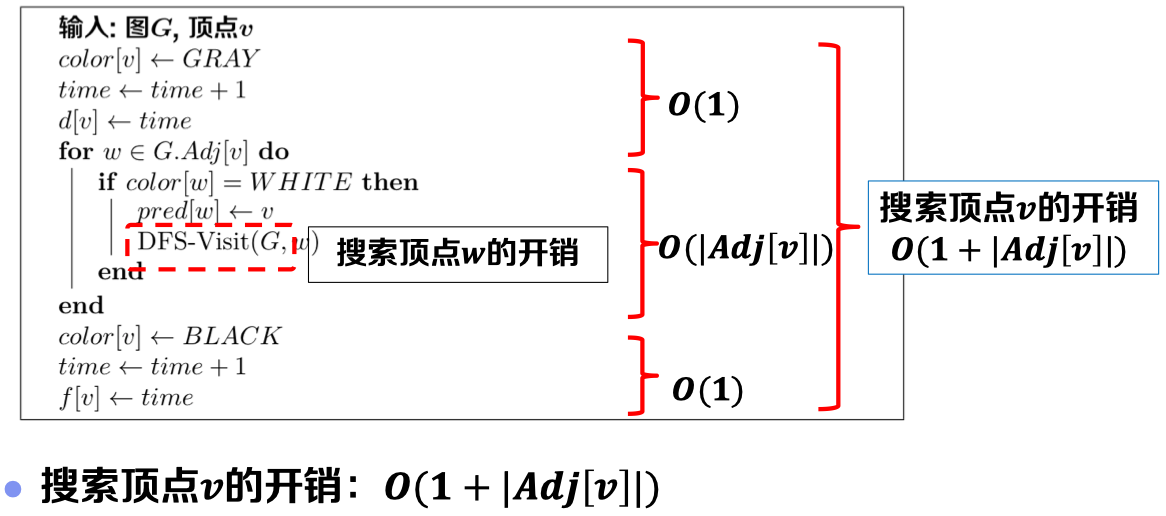
结合握手定理，可得总时间复杂度：
$𝑶(\sum_{v\in V}(1+|Adj[v]|))=𝑶(|V|)+\sum_{u\in V} (|Adj[v]|)=𝑶(|V|+|E|)$

3.6 算法性质：

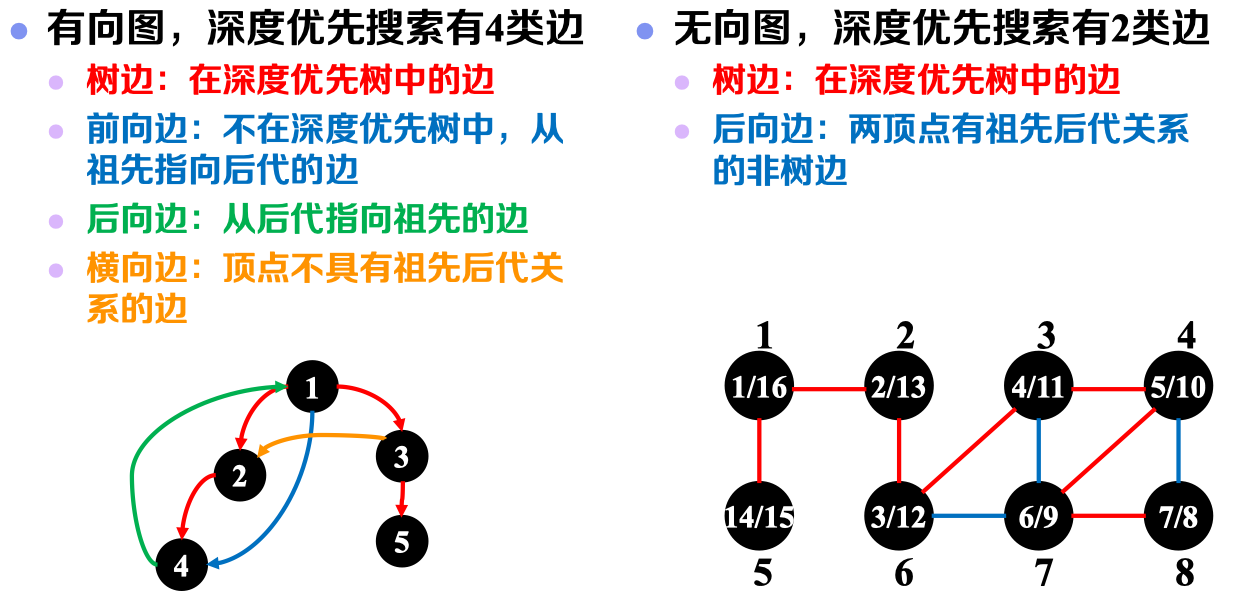
1）深度优先树：与BFS类似，结合𝒑𝒓𝒆𝒅数组可得到一棵深度优先树。据此，可将图中的边分为树边与非树边。
2）后向边：不是树边，但两顶点在深度优先树中是祖先后代关系。

在无向图中，非树边一定是后向边；

3）括号化定理：

点v发现时刻 $d[v]$ 和结束时刻 $f[v]$ 构成区间 $(d[v],f[v])$ ；
任意两点 $v,w$ 必然满足以下情况之一：
$(d[v],f[v])\subseteq (d[w],f[w])\to $→ w是v的后代；
$(d[v],f[v])\cap (d[w],f[w])=\emptyset\to$ → v和w均不是对方后代
P.s：括号化定理是基于区间标记解决可达性查询的核心思想。
4）白色路径定理：
在深度优先树中，顶点v是w的祖先⇔在v被发现前，从v到w存在全为白色顶点构成的路径。

4. 有向图 & 无向图对比:

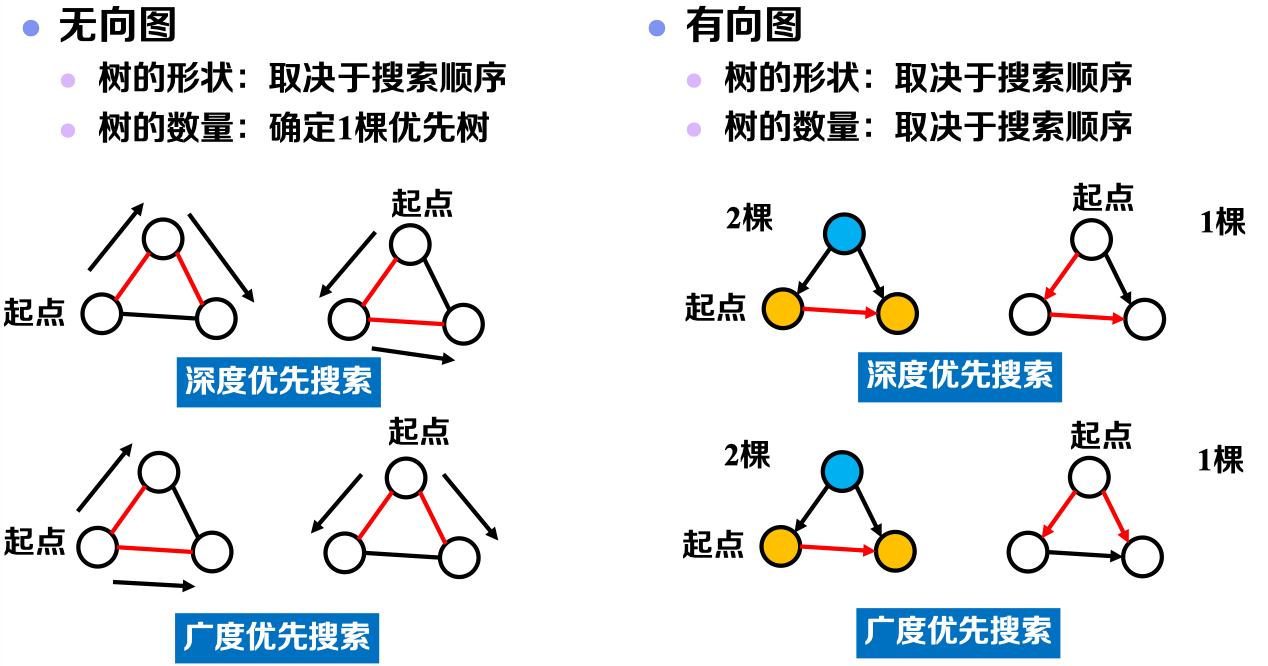
在之前的部分，我们主要以无向图作为研究对象，而在该节我们将对有向图展开讨论。需要注意的是，无向图其实质可以认为是一种边具有双向连通性的特殊的有向图。因此，我们在本节仅讨论有向图与无向图在DFS中性质的一些差异，BFS中的差异可类比得到。

MoCuishle