本文主要介绍图搜索算法(DFS & BFS)的应用实例,其包括:拓扑排序、环路检验和强连通分量计算。
本章主要介绍强连通分量计算问题~
本文内容提纲:
- 拓扑排序
- 环路检验
- 强连通分量计算
1. 概念:连通分量 & 强连通分量:
在之前的文章中介绍了连通分量的定义,如下:
连通分量:根据是否连通(任意对顶点互相可达)将顶点进行分组,相互可达的顶点集称为连通分量。
相较于连通分量,强连通分量(Strongly Connected Components,SCC)有如下特点:
强连通分量:1)有向图中,一个强连通分量是顶点的子集;2)强连通分量中任意两点相互可达;3)满足最大性:加入新顶点,不保证相互可达。
2. 应用背景:
强连通分量是图算法中一个重要的概念,在众多实际应用中也有大量的实际应用,例如:社交圈子的划分、可达性查询时对于原始图数据的简化等。在此,我们并不详细展开介绍。
3. 问题定义:
定义:强连通分量问题
- 输入:有向图;
- 输出:图的所有强连通分量;
4. 算法框架与实例:
由于该问题较难理解,我们首先介绍算法的整体框架——运行过程,以及一个实例演示:
- 把原图中各条边反向,得到反向图
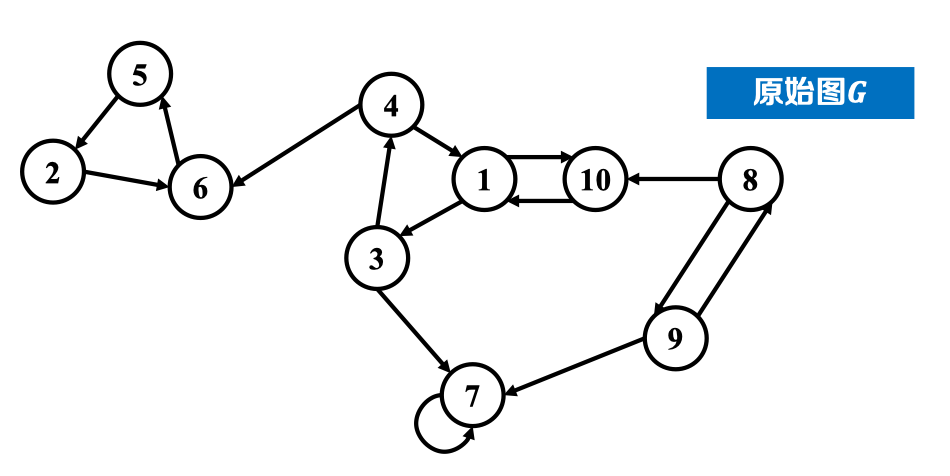
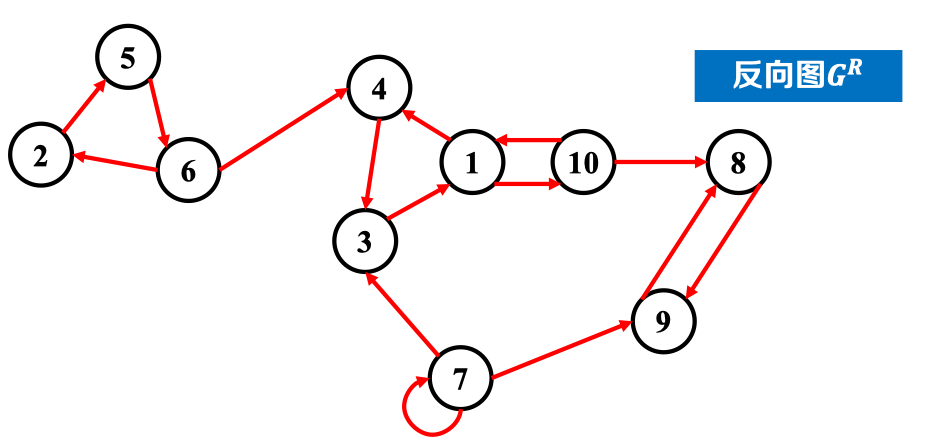
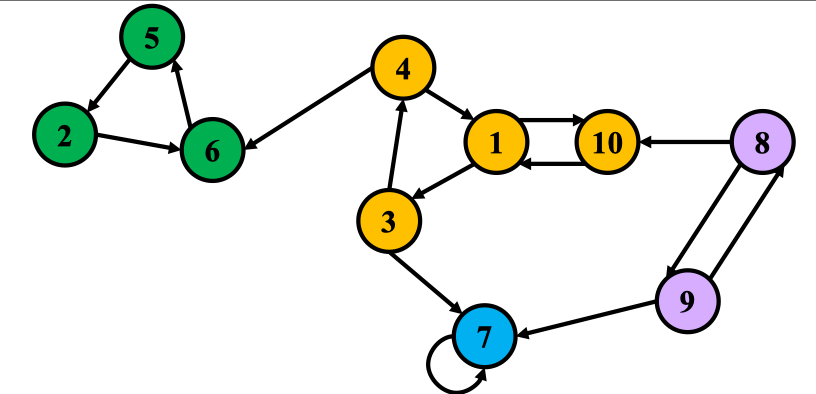
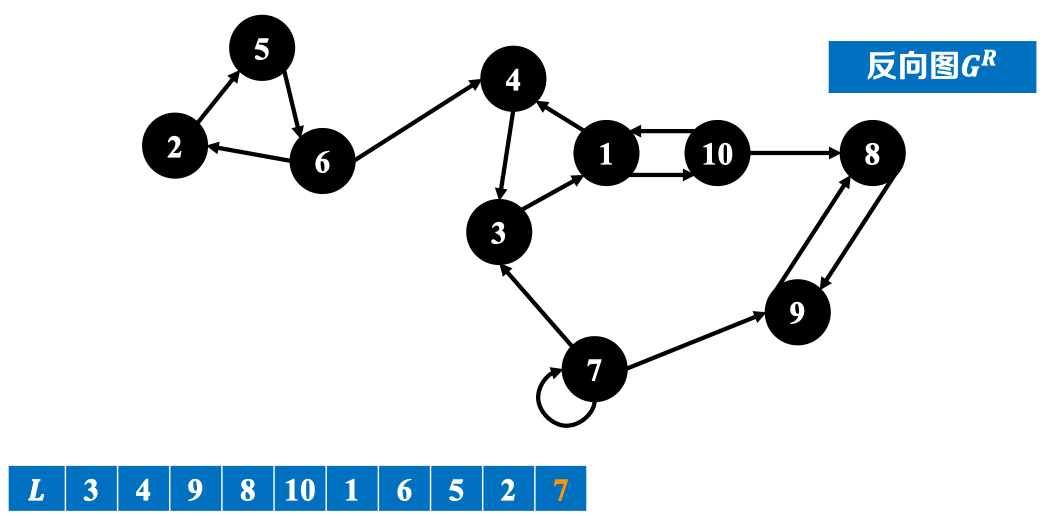
- 在反向图上执行DFS,得到顶点完成时刻顺序;
(实例中根据节点编号顺序开始执行DFS,即首先从1节点开始,之后2节点,最后7节点)
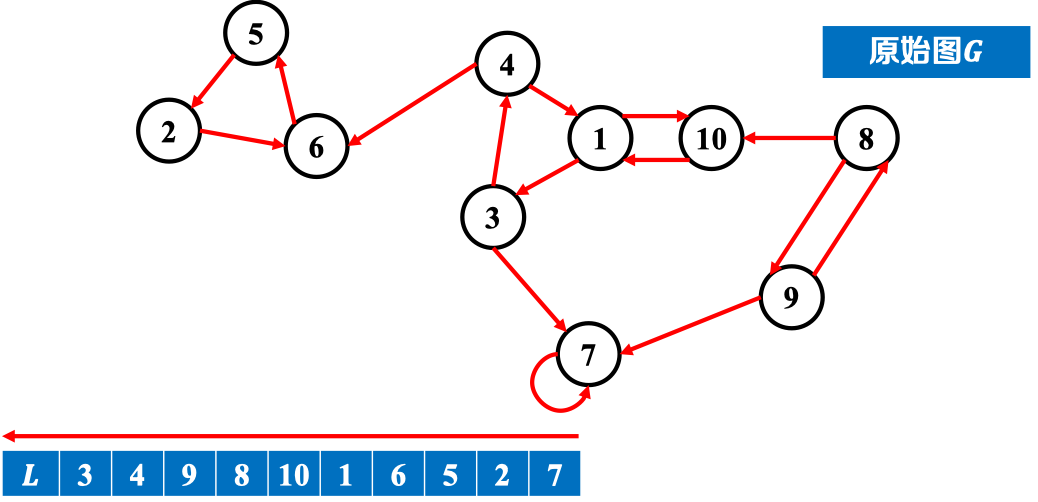
- :在原图上按逆序执行DFS,得到强连通分量。
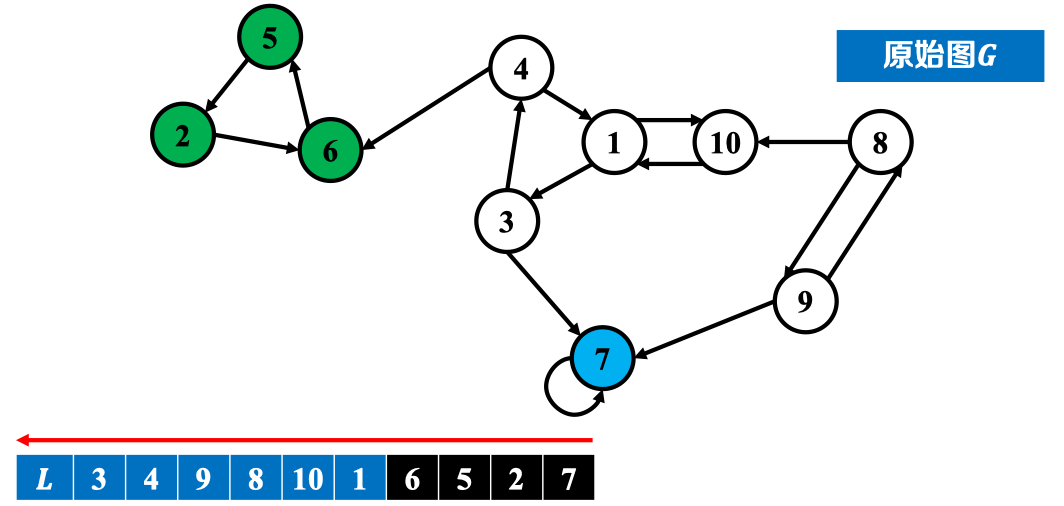
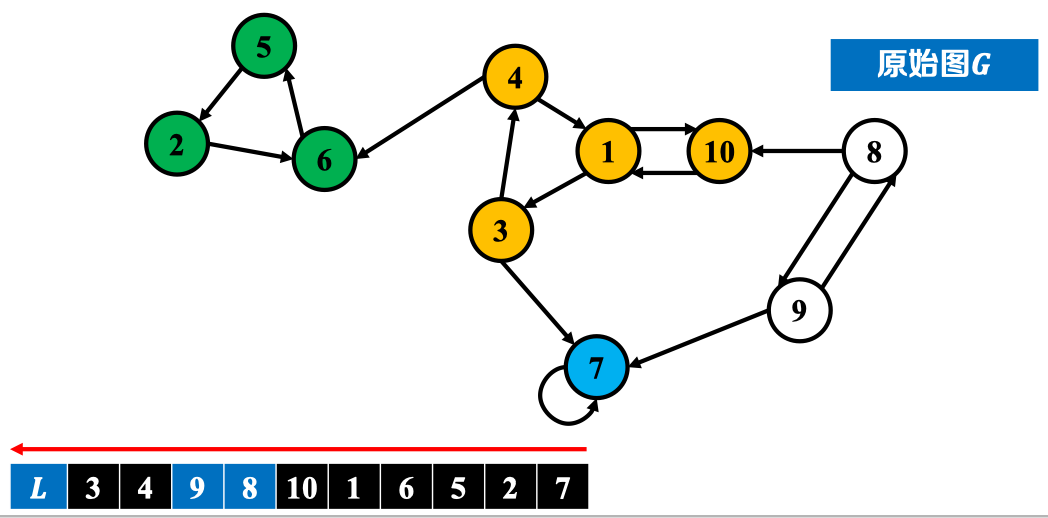
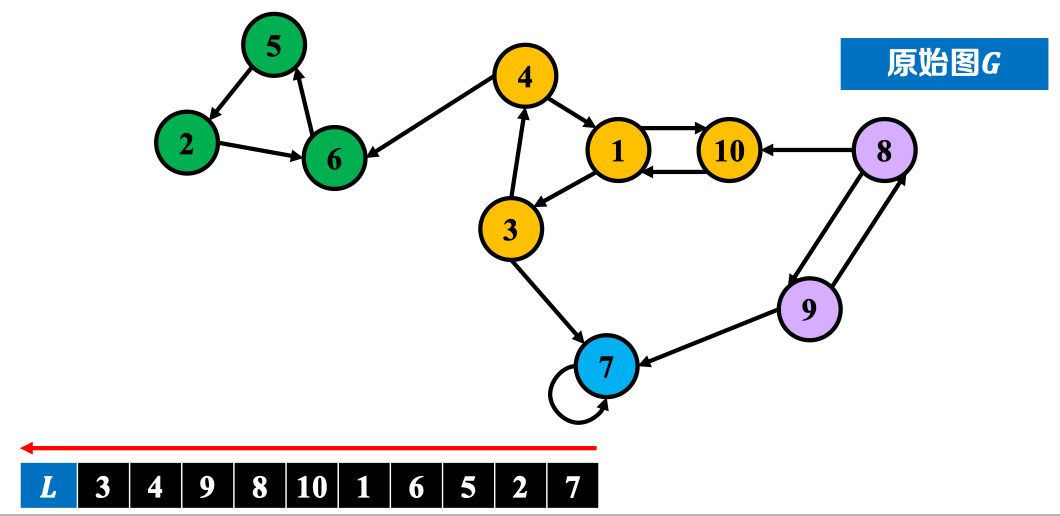
5. 算法伪代码:

在搜索过程中得到可参考基于深度优先策略解决拓扑排序问题中的方法:

显然,该算法复杂度为
6. 算法分析:
在介绍算法正确性之前,我们先引入强连通分量图的概念及其性质:
强连通分量图:把强连通分量看作一个点,得到的有向图。
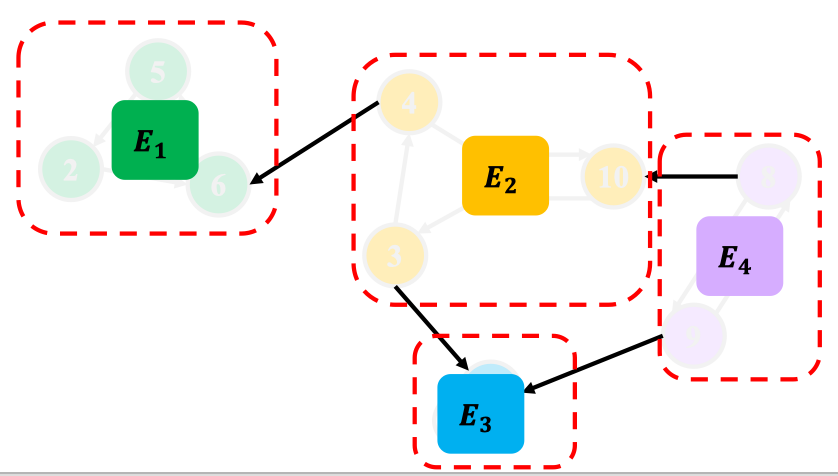
- 性质:一定是有向无环图——由“最大性”易证得。
:中出度为0的点,我们称之为。
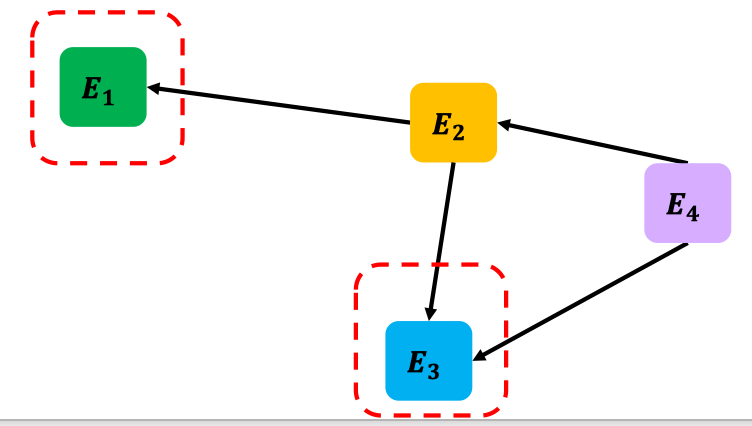
- 性质1:中至少存在一个;
- 性质2:删除,会产生新的;
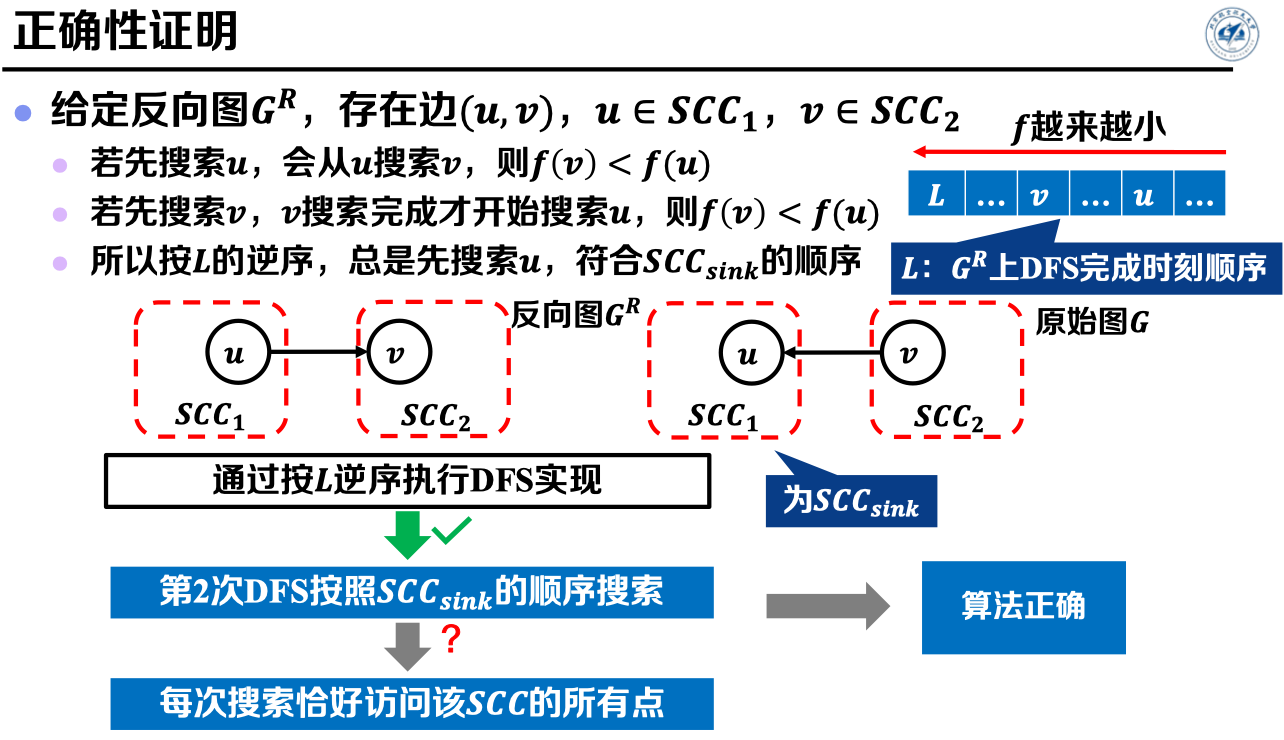
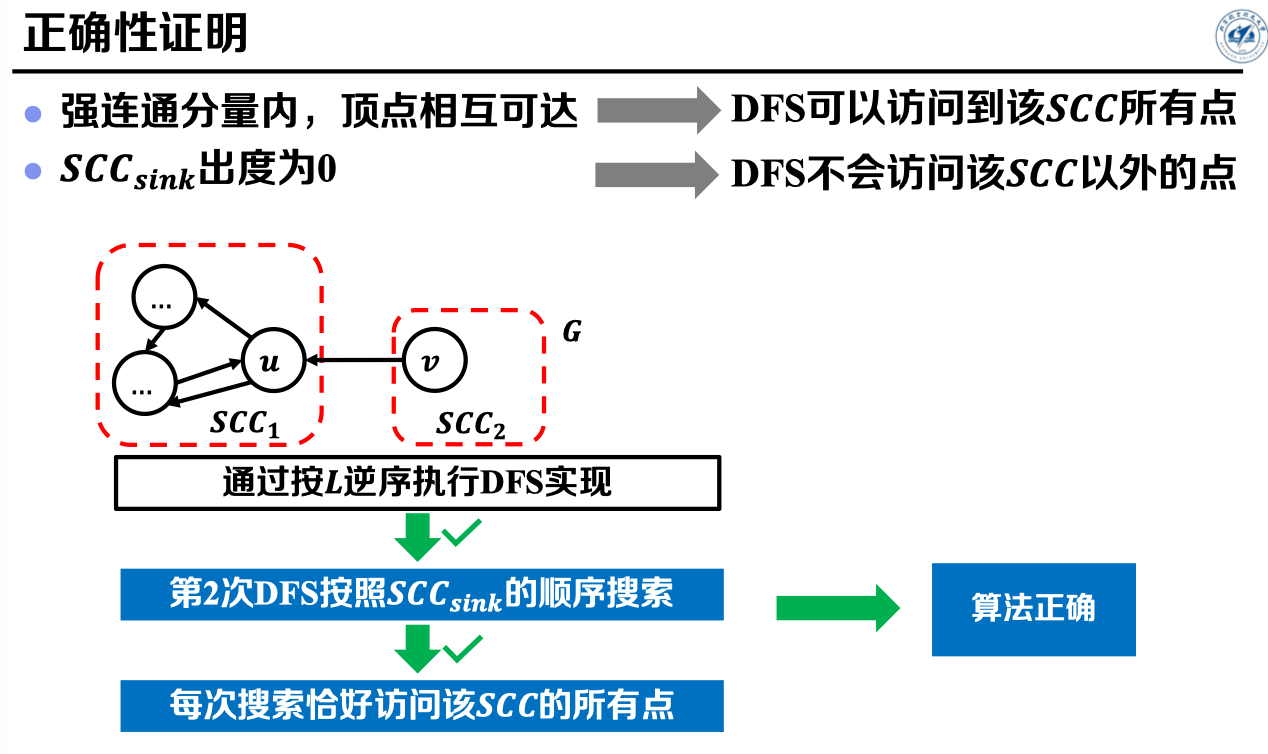
结合以上性质观察算法第2次DFS,可知:第2次DFS按照的顺序搜索,并且每次搜索恰好访问该SCC的所有点。