MoCuishle

本文主要介绍图搜索算法（DFS & BFS）的应用实例，其包括：拓扑排序、环路检验和强连通分量计算。
P.s：考虑到强连通分量算法是一个较为难以理解的算法，故将强连通分量问题放在下章单独介绍。

本文内容提纲：

• 拓扑排序
• 环路检验
• 强连通分量计算（见下章）

1. 拓扑排序：

首先需要明确的是，拓扑排序主要用于确定事件间流程顺序，而有向图则是对事件间依赖关系的一种准确的建模。因此，本文对拓扑排序的讨论主要基于有向无环图（Directed Acyclic Graph，DAG）。此处强调无环图是因为，一旦图中出现环路，说明事件之间存在相互依赖关系，即难以确定事件间的流程顺序。这也引发出对于图中环路检验的一种方法，我们将在环路检验部分进行介绍。

定义：拓扑排序：

• 输入：有向无环图$G=(V,E)$；
• 输出：图顶点$V$的拓扑序$S$，满足：对图中任意有向边$(u,v)$，在$S$中$u$在$v$之前。
• 拓扑序不唯一

1.1. 基于广度优先（BFS）策略：

1）算法思想：

从节点度数入手——若顶点入度为0，说明所对应事件无制约条件，可直接完成。因此算法思想如下：

• 完成入度为0的节点所对应的事件；
• 删除完成事件，产生新的入度为0节点，继续完成。

具体而言，借助队列这一数据结构，进行实现：
（1）将图中入度为0的节点全部压入队列；
（2）若队列非空，则将队首元素出队列，视为完成该节点对应事件。同时，删除图中该节点对应节点及其出边；
（3）将图中新产生入度为0的节点，压入队列。
（4）反复执行（2）、（3）直至队列为空。

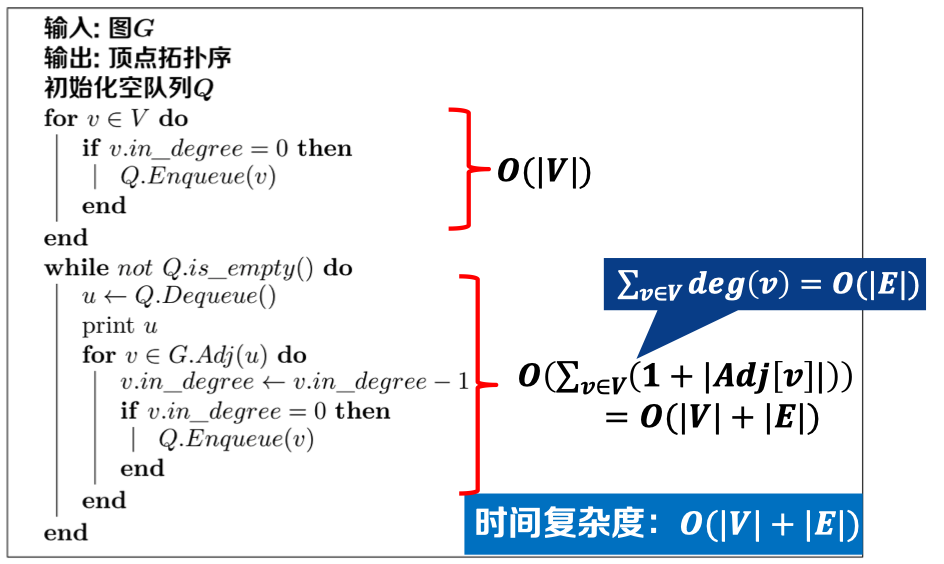
2）算法伪代码：

3）算法复杂度分析：

1.2 基于深度优先（DFS）策略：

1）算法思想：

根据DFS算法我们可：搜索深度越深，顺序越靠后；而对于深度越深的节点：发现时刻越晚，完成时刻越早（参考DFS中对节点标记发现时刻与完成时刻标记）。若我们依据发现时刻顺序得到拓扑序，很容易得到反例，因此，依据发现时刻顺序的思路并不可行；因而，我们考虑能否按照完成时刻的逆序进行拓扑排序。以下给出一个实例：

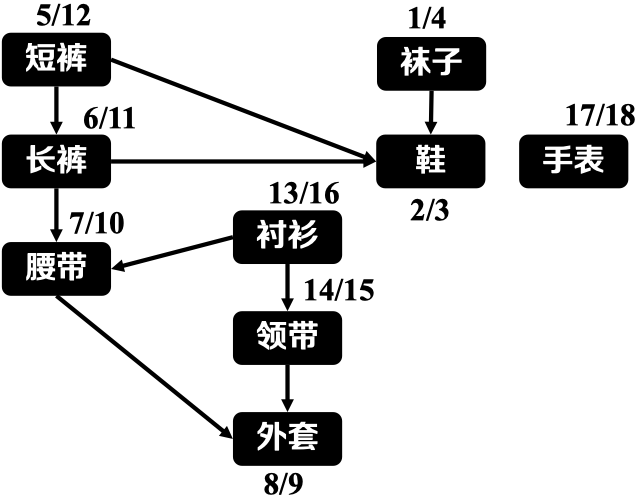
所得拓扑序：手表、衬衫、领带、短裤、长裤、腰带、外套、袜子、鞋

2）算法分析：

下图给出了该方法的正确性证明：

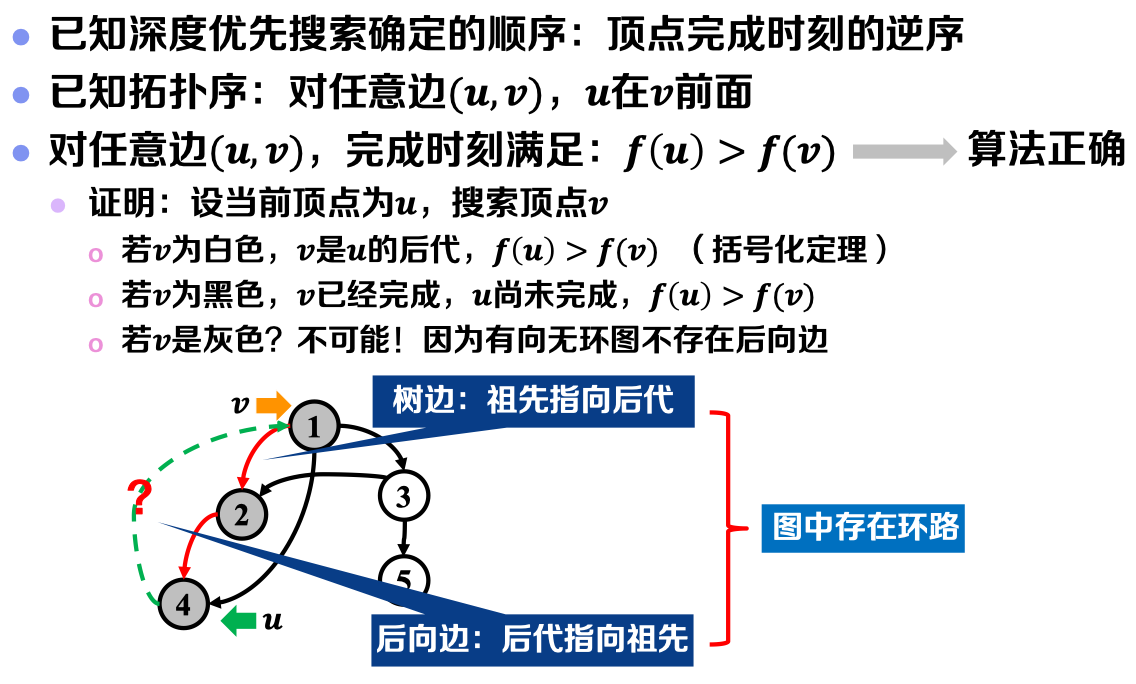
3）算法伪代码：

为了在搜索过程中得到按完成时刻顺序排列的顶点，可参考如下伪代码：

之所以引入$L'$是因为，对于有向图DFS，得到的可能是一个深度优先森林，因此引入$L'$。

4）算法复杂度分析：

显然，基于DFS策略的拓扑排序其复杂度与DFS算法一致：$O(|V|+|E|)$

1.3 小结：

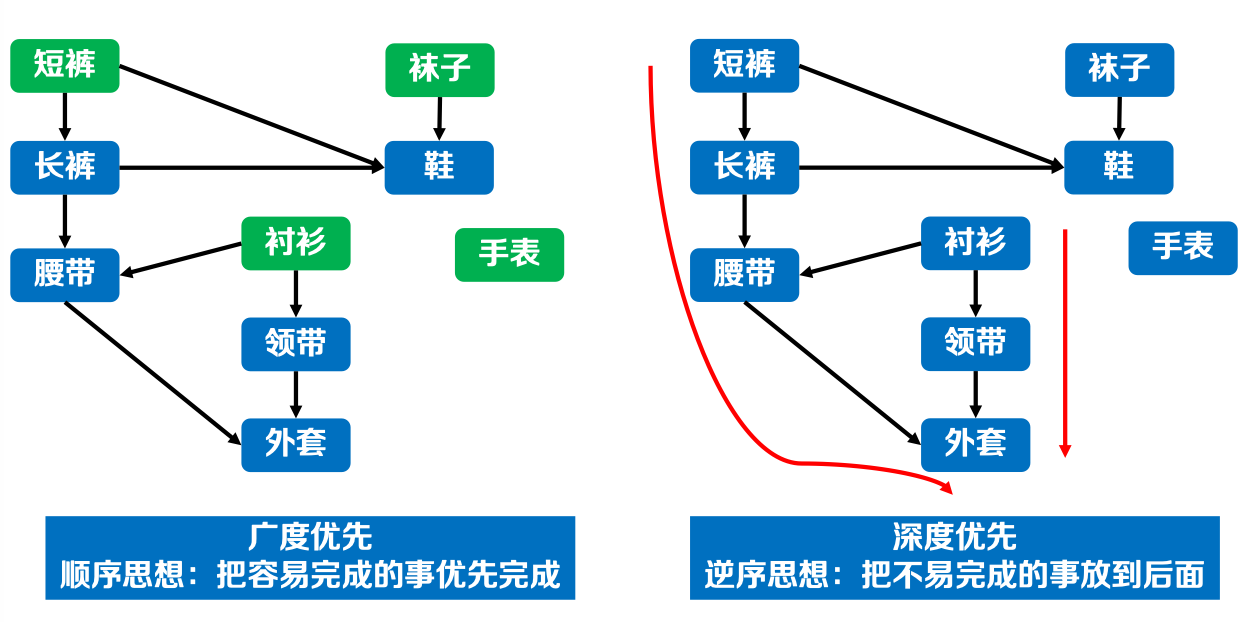
2. 环路检验：

定义：有向图中环路的存在性判断：

• 输入：有向图$G=(V,E)$；
• 输出：图$G$中是否存在环。
  目前，有向图中环路的存在性判断问题主要存在两种解决思路：1）基于深度优先搜索边的性质；2）利用拓扑排序的性质。

2.1 基于深度优先搜索边的性质：

1）算法思路

对于有向图，深度优先搜索时存在以下边的种类：

• 树边：在深度优先树中的边；
• 前向边：不在深度优先树中，从祖先指向后代的边
• 后向边：从后代指向祖先的边
• 横向边：顶点不具有祖先后代关系的边
  

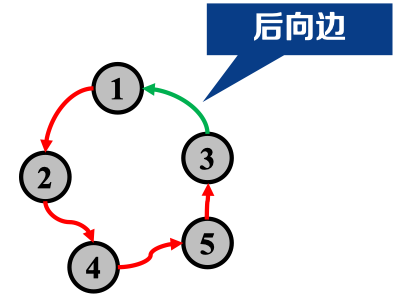
经过证明，我们不难得到：有向图存在环路$\iff$搜索时出现后向边

2）算法伪代码：

3）算法复杂性分析：

显然，基于DFS策略的环路检验其复杂度与DFS算法一致：$O(|V|+|E|)$

2.2 利用拓扑排序的性质：

根据之前拓扑排序算法的介绍（基于BFS）：算法首先寻找一个入度为0的顶点，将该顶点从图中删除（即放进一个队列里存着，这个队列的顺序就是最后的拓扑排序）；并将该结点及其所有的出边从图中删除（即该结点指向的结点的入度减1）；最终若图中节点非空且当前图中不存在无前驱的顶点，则说明该有向图中必然存在环