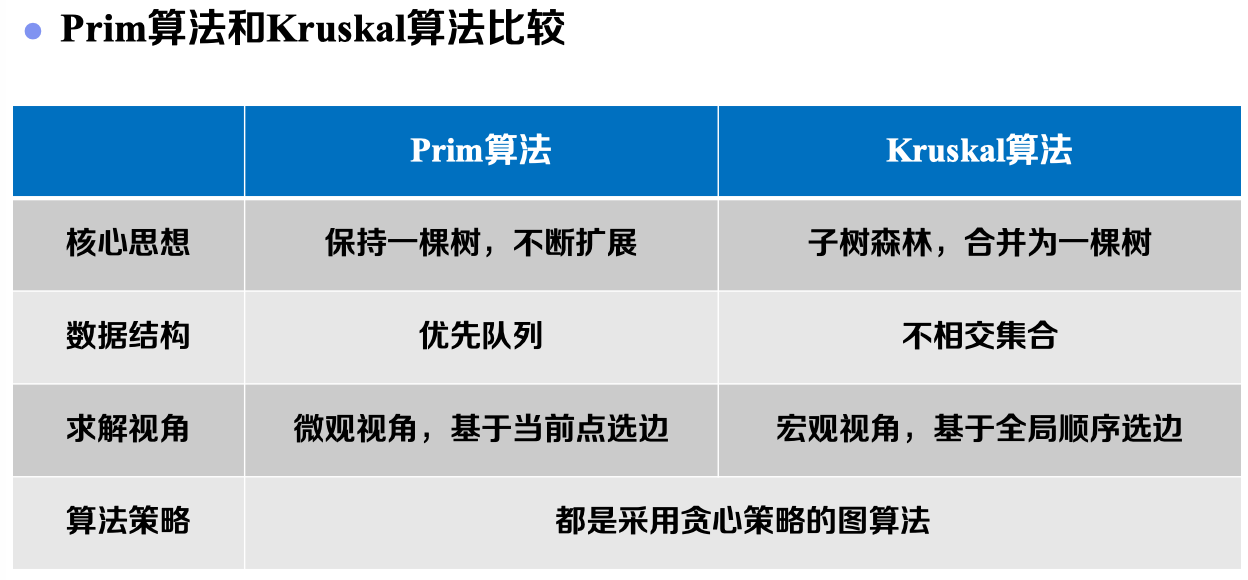
最小生成树问题是图算法问题中一类经典的问题，其在大量其他的图算法问题中也有广泛的应用。最小生成树问题，其核心是“贪心策略”在图算法中的应用，并由此产生了两类经典的最小生成树算法：Prim算法&Kruskal算法。

本文内容概要：

  • 最小生成树问题背景及通用框架
  • Prim算法
  • Kruskal算法

1. 最小生成树问题背景及通用框架

1.1 问题引入：

实例：城市间道路修建问题——需要修建道路连通城市，各道路花费不同，求解连通各城市的最小花费是多少？

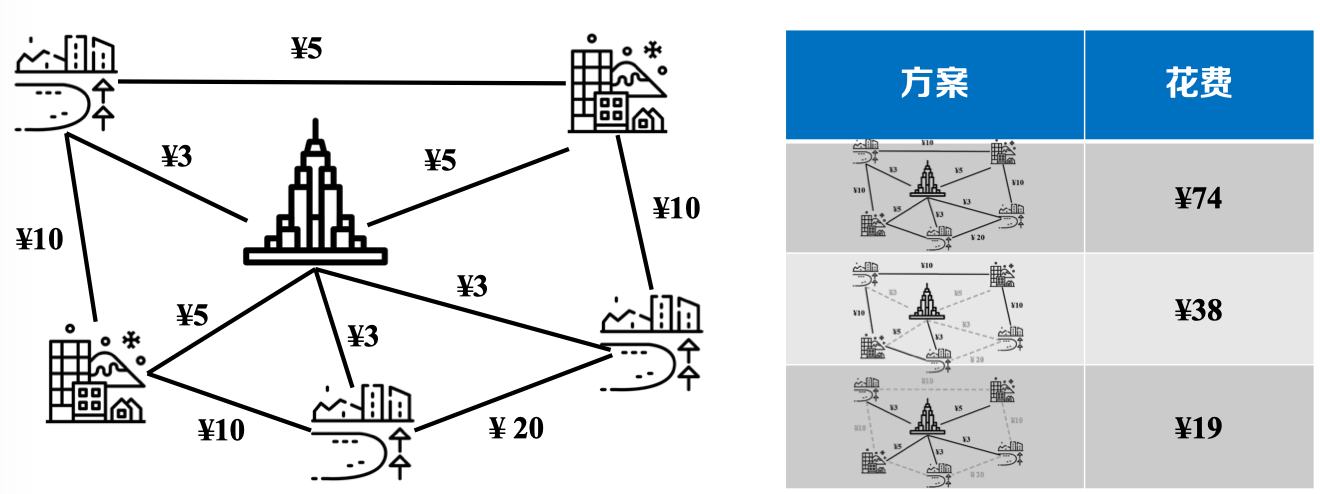
1.2 问题定义：

定义-1.1 子图（Subgraph）： 如果V′⊆V,E′⊆EV'\subseteq V, E'\subseteq E，则称图G′=(V′,E′)G'=(V',E')是图G=(V,E)G=(V,E)的一个子图；
定义-1.2 生成子图（Spanning Subgraph）： 如果V′=V,E′⊆EV'= V, E'\subseteq E，则称图G′=(V′,E′)G'=(V',E')是图G=(V,E)G=(V,E)的一个生成子图；

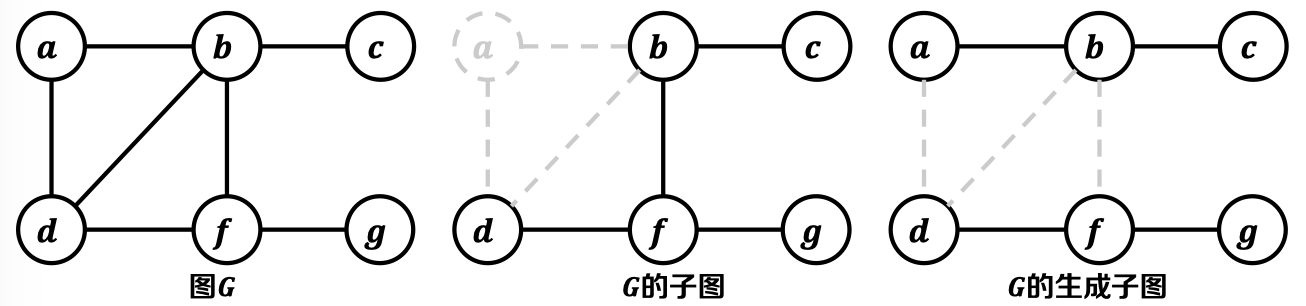
定义-1.3 生成树（Spanning Tree）： 图T′=(V′,E′)T'=(V',E')是无向图图G=(V,E)G=(V,E)的一个生成子图，并且是连通、无环的（树）；

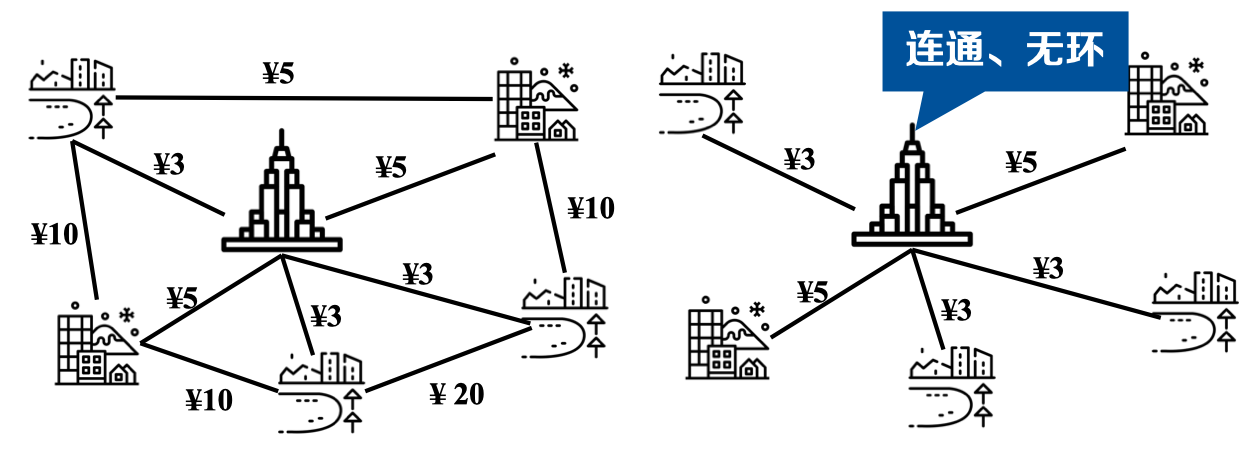
P.s：权重最小的生成树可能不唯一！（但如果各条边权重各不相同，则最小生成树唯一）

定义-1.4 最小生成树问题（Minimum Spanning Tree Problem）：

  • 输入：连通的无向图G=(V,E,W)G=(V,E,W)，其中w(u,v)∈Ww(u,v)\in W表示边(u,v)(u,v)的权重；
  • 输出：无向图G=(V,E,W)G=(V,E,W)的最小生成树T=(VT,ET)T=(V_T,E_T)，
    * 优化目标：min∑e∈ETw(e)min \sum_{e\in E_T} w(e)
    * 约束条件：s.t. VT=V,ET⊆Es.t. \ V_T=V,E_T\subseteq E

1.3 通用框架


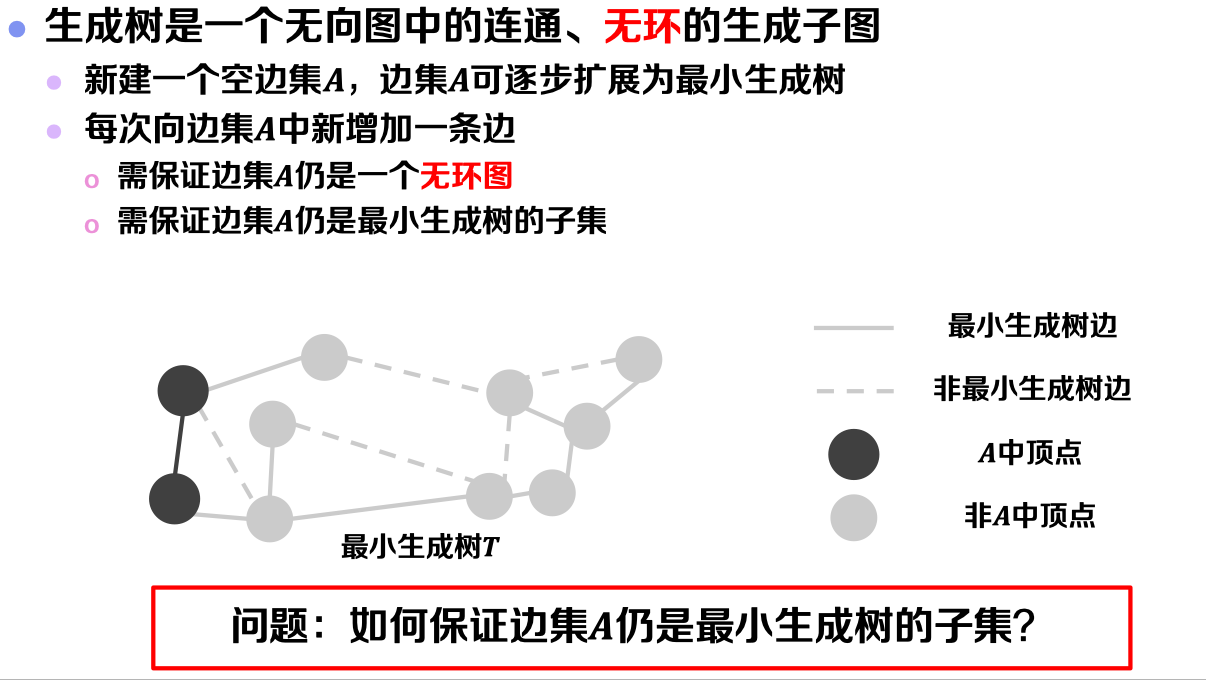
需要注意的是，由于最小生成树是原图的一个生成子图。因此，求解最小生成树，其实质是求原图中属于最小生成树的边集。

问题1：如何保证边集𝑨仍是最小生成树的子集？
定义-1.5 安全边（Safe Edge）：
* 𝑨是某棵最小生成树𝑻边的子集，𝑨 ⊆ 𝑻
* 𝑨 ∪ {(𝒖, 𝒗)} 仍是 𝑻 边的一个子集，则称(𝒖, 𝒗)是𝑨的安全边

回答1：若每次向边集𝑨中新增安全边，可保证边集𝑨是最小生成树的子集。可将框架具体为：

问题2：如何有效辨识安全边？
定义-1.6 割（Cut）： 图𝑮 =(𝑽, 𝑬)是一个连通无向图，割(𝑺, 𝑽 − 𝑺)将图𝑮的顶点集𝑽划分为两部分。

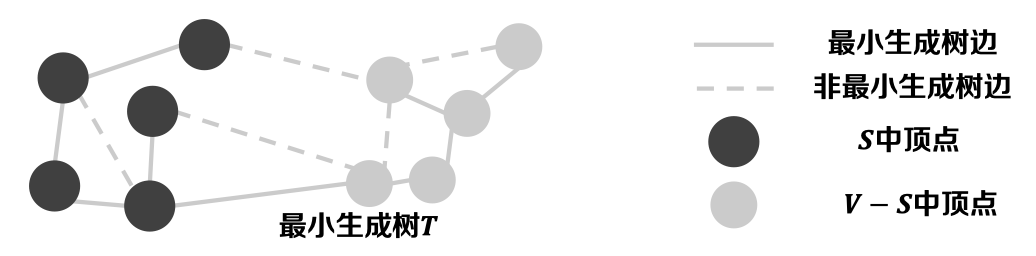
定义-1.7 横跨（Cross）： 给定割(𝑺, 𝑽 − 𝑺)和边(𝒖, 𝒗)，𝒖 ∈ 𝑺, 𝒗 ∈ 𝑽 − 𝑺，称边横跨(𝒖, 𝒗)割(𝑺, 𝑽 − 𝑺)

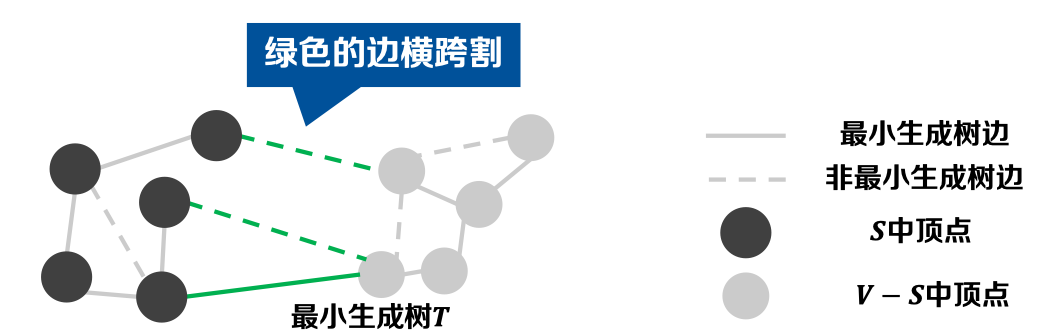
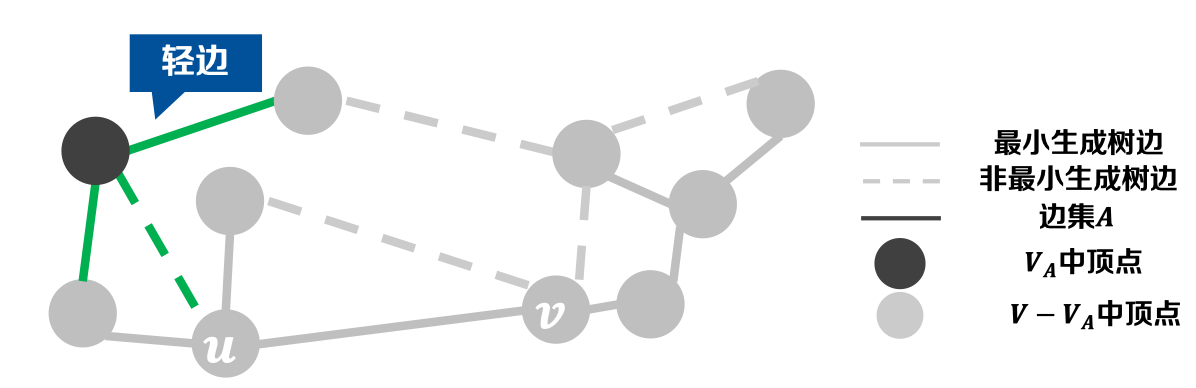
定义-1.8 轻边（Light Edge）： 横跨割的所有边中，权重最小的称为横跨这个割的一条轻边。

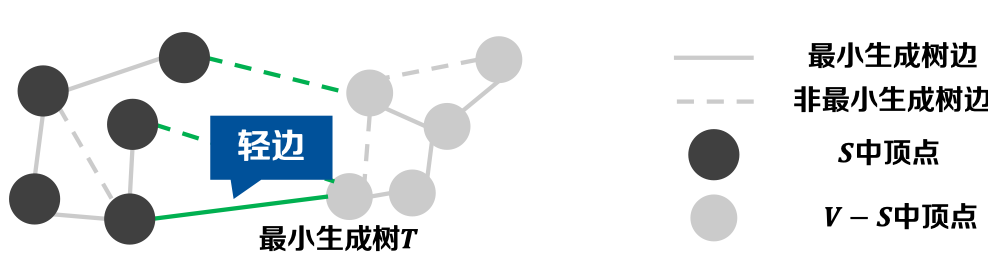
定义-1.9 不妨害（Respect）： 如果一个边集𝑨中没有边横跨某割，则称该割不妨害边集𝑨。

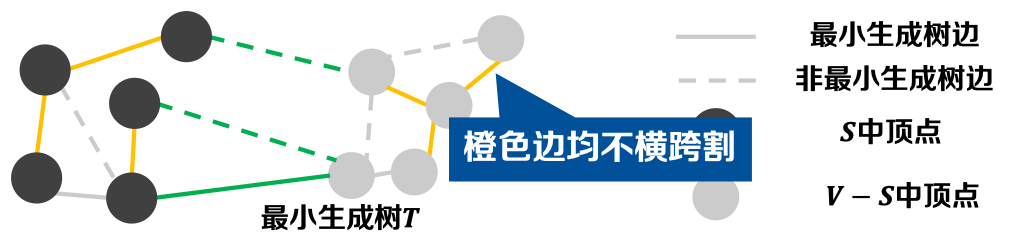
安全边辨识定理：
前提：给定图𝑮 =(𝑽, 𝑬 )是一个带权的连通无向图，令𝑨是边集𝑬的一个子集，且𝑨包含在图𝑮的某棵最小生成树中。
内容：
* 若割(𝑺, 𝑽 − 𝑺)是图𝑮中不妨害边集𝑨的任意割，且(𝒖, 𝒗)是横跨该割的轻边；
* 则对于边集𝑨，边(𝒖, 𝒗)是其安全边。

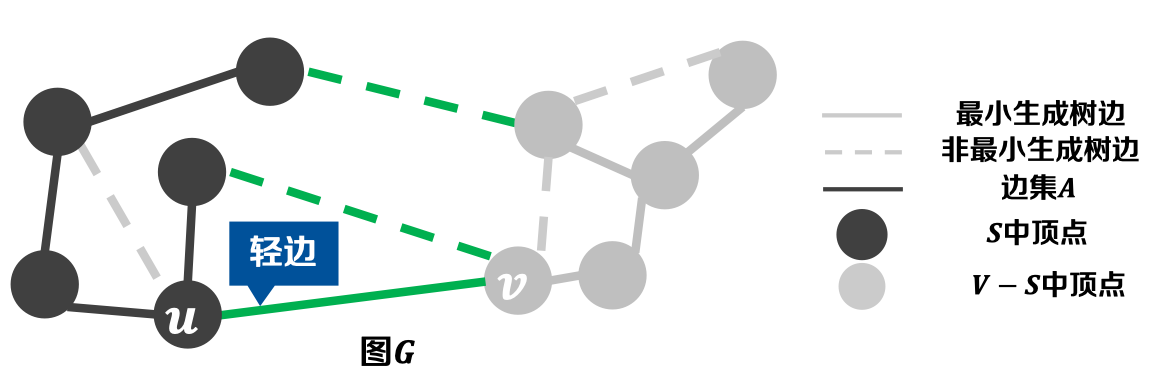
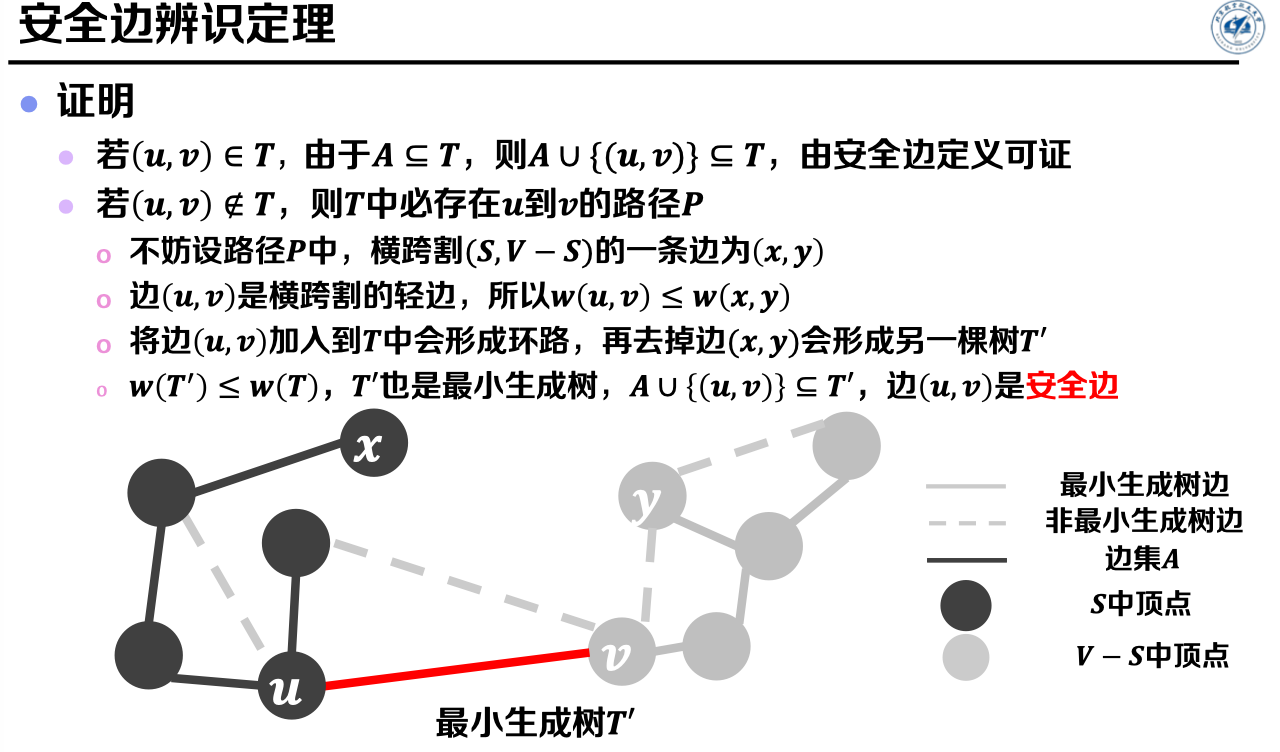
综上所述，我们可将通用框架作如下总结：

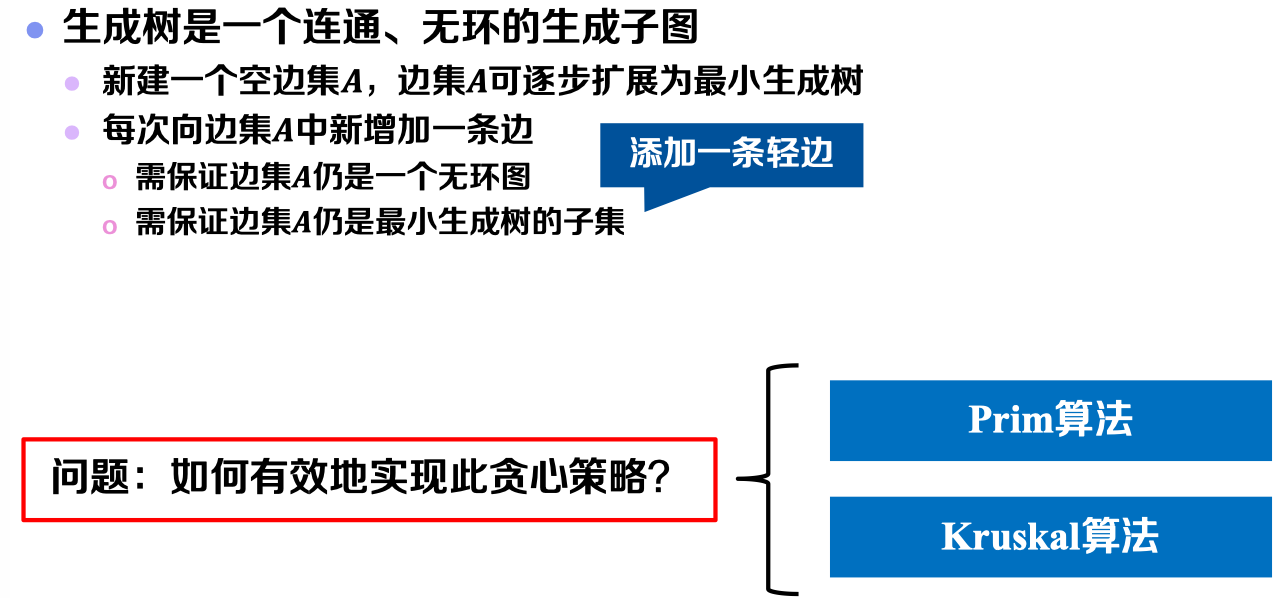
即：

  • 保证无环；
  • 找轻边。

2. Prim算法

Prim算法是我们以上总结的求解最小生成树通用框架策略的一种具体实现，具体而言该方法主要着眼于“节点”的角度。其思想概括如下：

  • 保证无环——始终保持一棵树
  • 找轻边——优先队列求轻边

2.1 算法思想：

  • 步骤1：选择任意一个顶点，作为生成树的起始顶点；
  • 步骤2：保持边集𝑨始终为一棵树，选择割(𝑽𝑨𝑽_𝑨 , 𝑽 − 𝑽𝑨𝑽_𝑨)；
  • 步骤3：选择横跨割(𝑽𝑨𝑽_𝑨 , 𝑽 − 𝑽𝑨𝑽_𝑨)的轻边，添加到边集𝑨中；
  • 步骤4：重复步骤2和步骤3，直至覆盖所有顶点。

2.2 算法实现：

为便于算法描述，仍借用辅助数组标记各节点状态以及横跨割的边的权重：

  • 𝒄𝒐𝒍𝒐𝒓数组：表示顶点状态
    • Black——节点已覆盖，u∈𝑽𝑨u\in 𝑽_𝑨
    • White——节点未覆盖，u∈𝑽−𝑽𝑨u\in 𝑽-𝑽_𝑨
  • 𝒑𝒓𝒆𝒅记录前驱节点：
    • (𝒑𝒓𝒆𝒅[𝒖], 𝒖)即为最小生成树的边
  • 𝒅𝒊𝒔𝒕记录横跨割(𝑽𝑨𝑽_𝑨 , 𝑽 − 𝑽𝑨𝑽_𝑨)的边的权重：
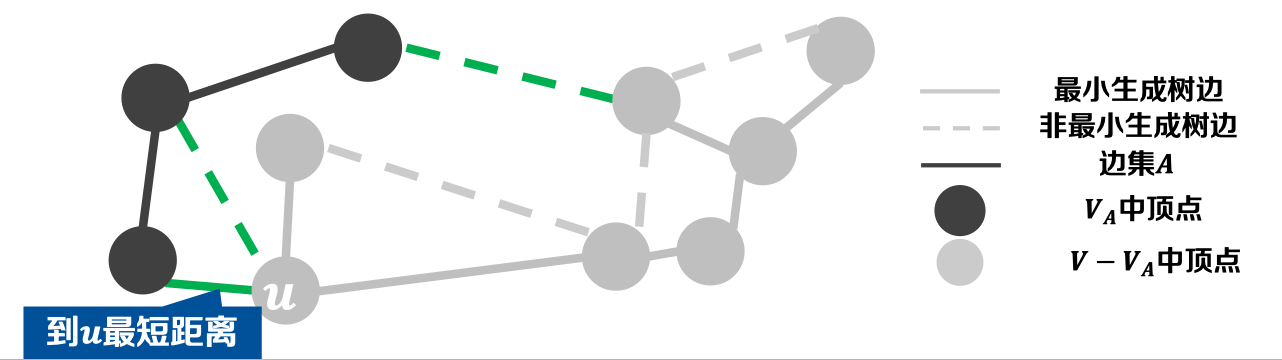
    • 𝒅𝒊𝒔𝒕[u]——顶点集𝑽𝑨𝑽_𝑨到顶点𝒖的最短距离，即：𝒅𝒊𝒔𝒕[u]=𝐦𝐢𝐧 {𝒘(𝒙, 𝒖)},∀𝒙∈𝑽𝑨𝑽_𝑨；
    • 轻边——𝐦𝐢𝐧{𝒅𝒊𝒔𝒕[𝒖]}, ∀𝒖 ∈ 𝑽−𝑽𝑨𝑽_𝑨

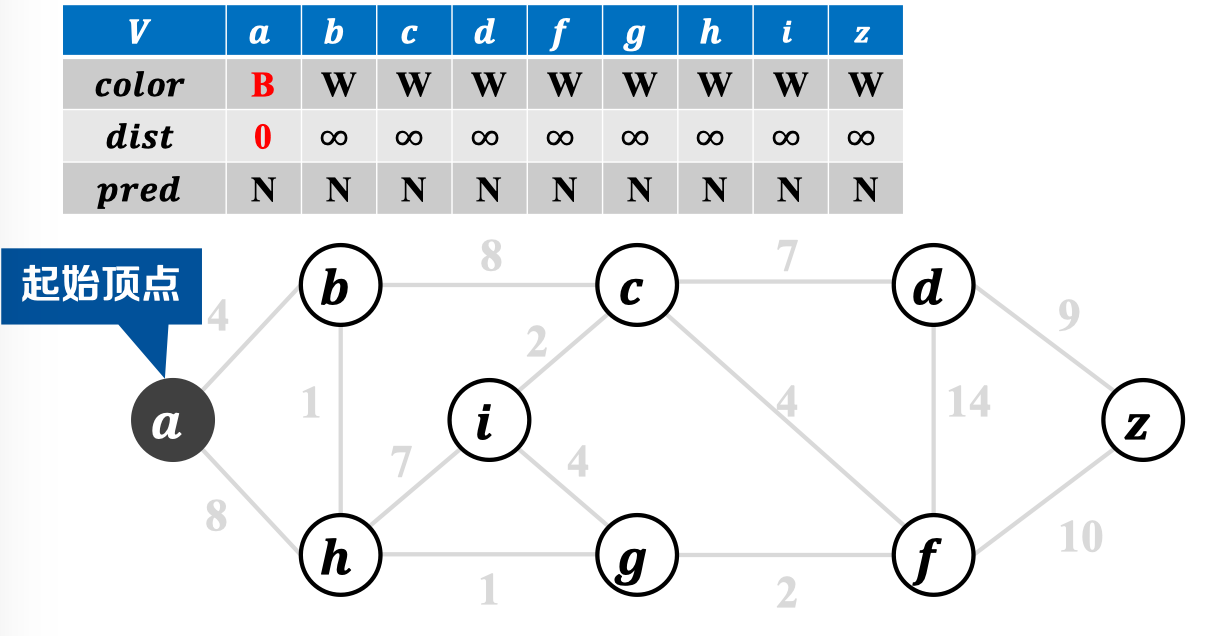
2.3 算法实例：

不妨设aa为起始节点：

在横跨割的候选边中选轻边，并加入边集中：

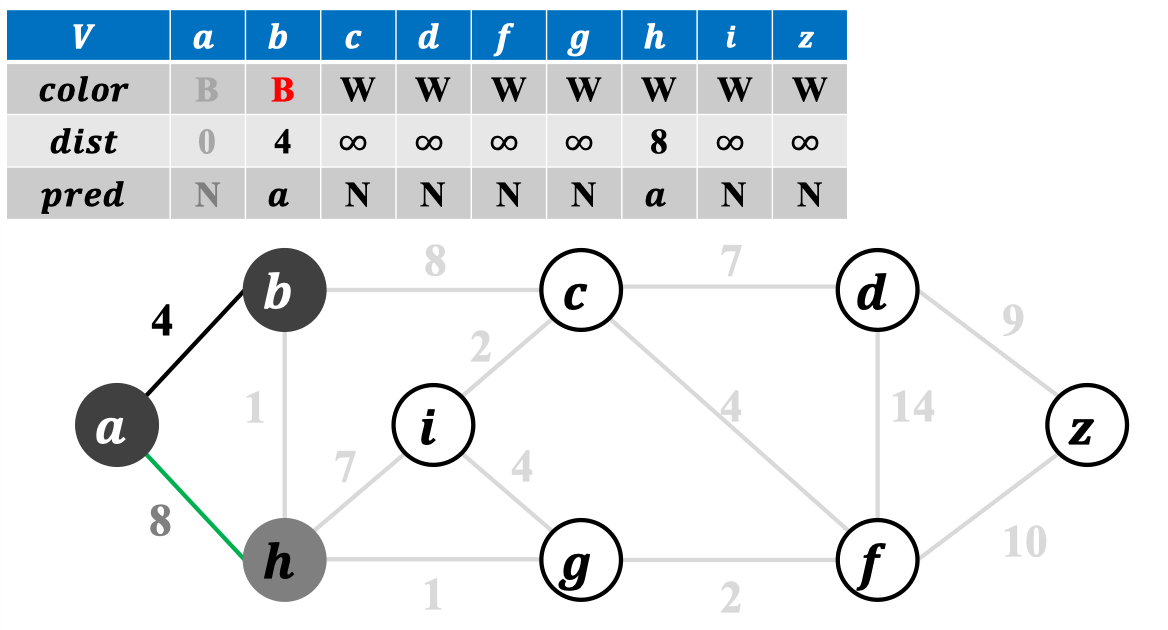
更新横跨割的候选边：

...
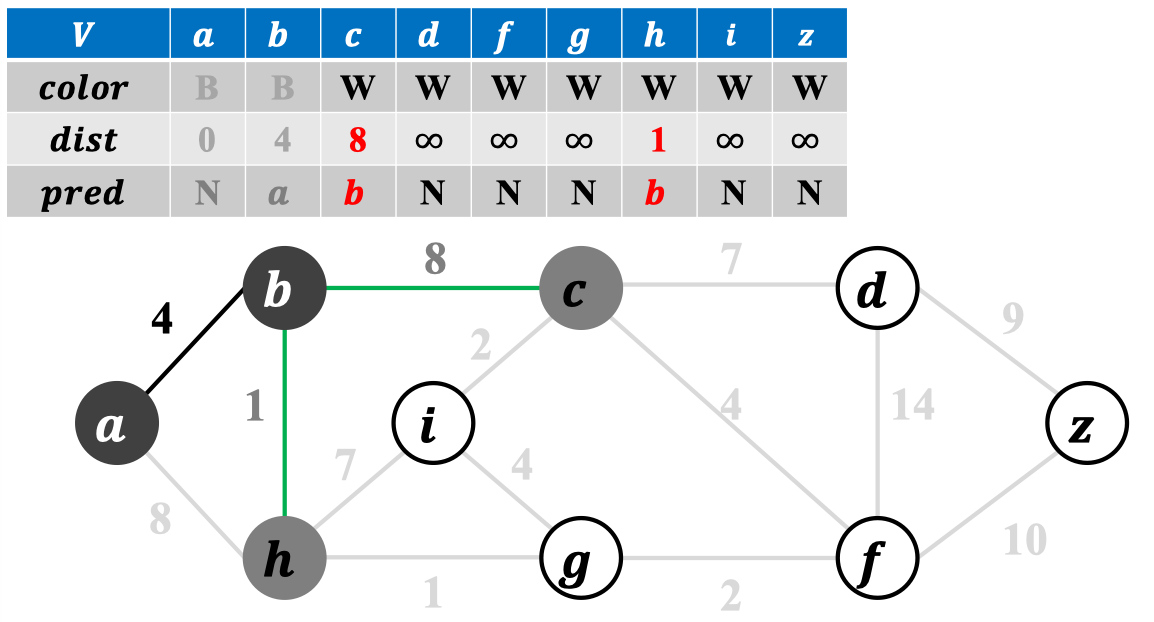
最终求得最小生成树：

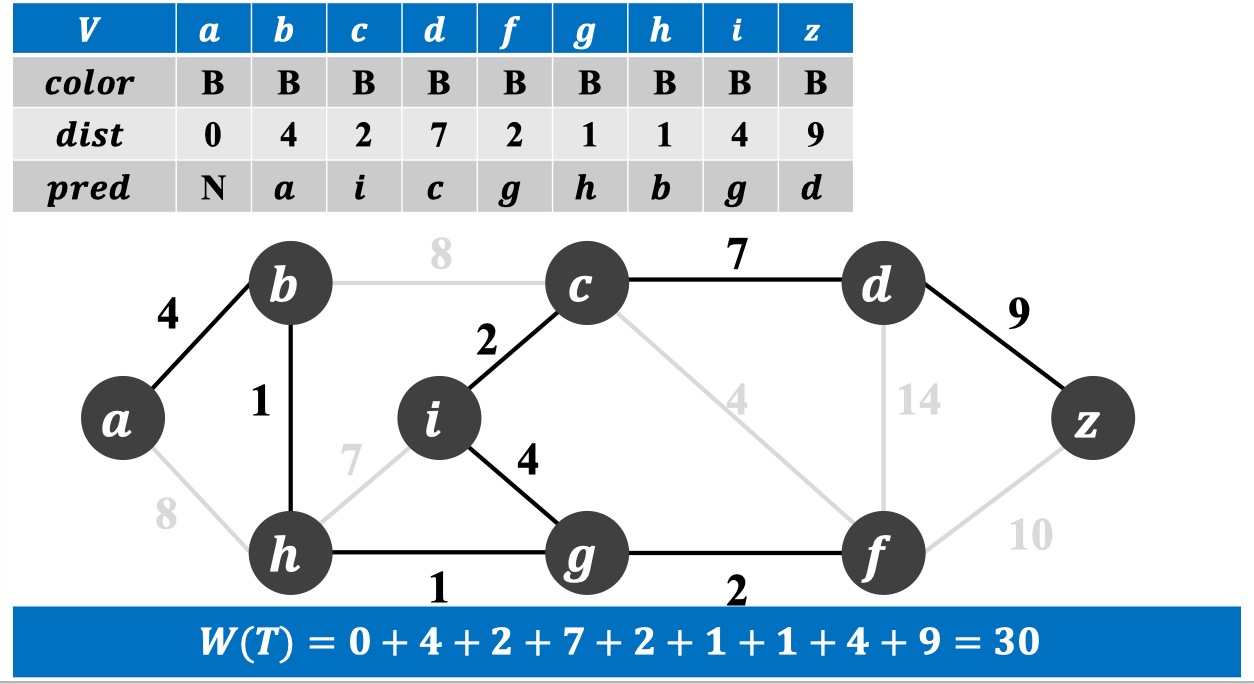
2.4 算法伪代码：

首先我们给出算法直观地伪代码，如下：


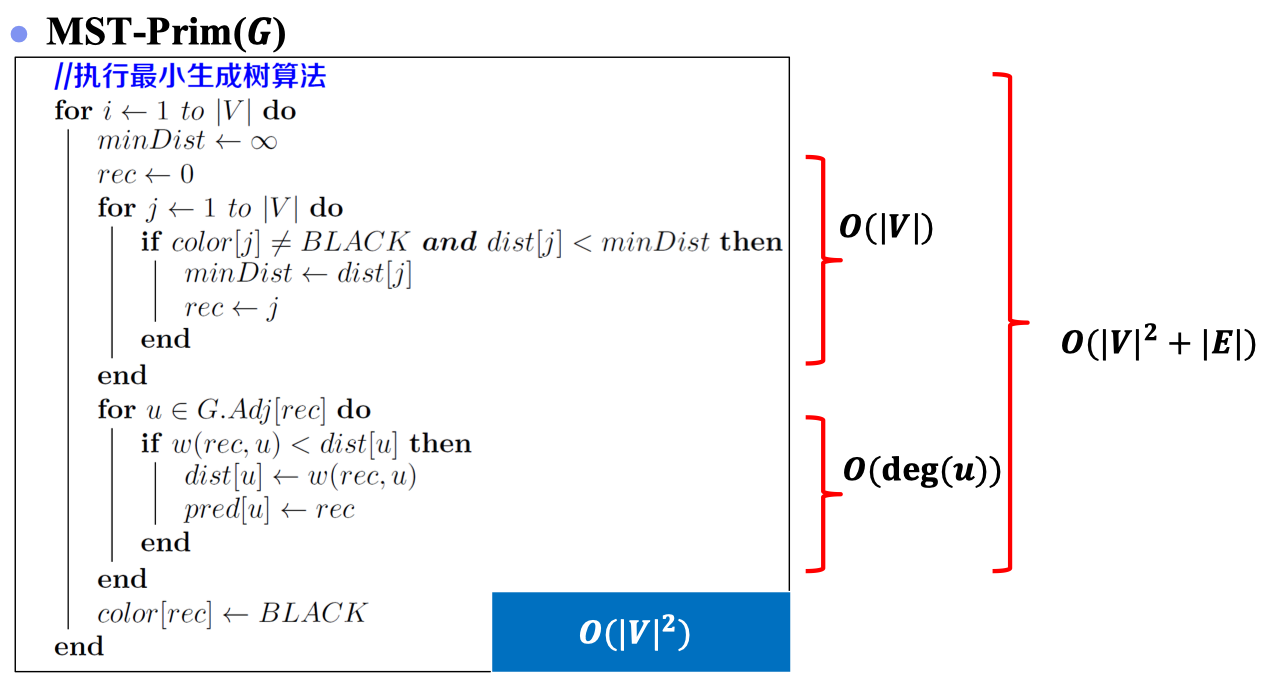
可见，直观地实现Prim算法，其复杂度为O(∣V∣2)O(|V|^2)。然而，我们发现：在找轻边的过程中，我们可以采用优先队列这一数据结构简化算法复杂度：
P.s：关于优先队列——通过二叉堆进行实现：

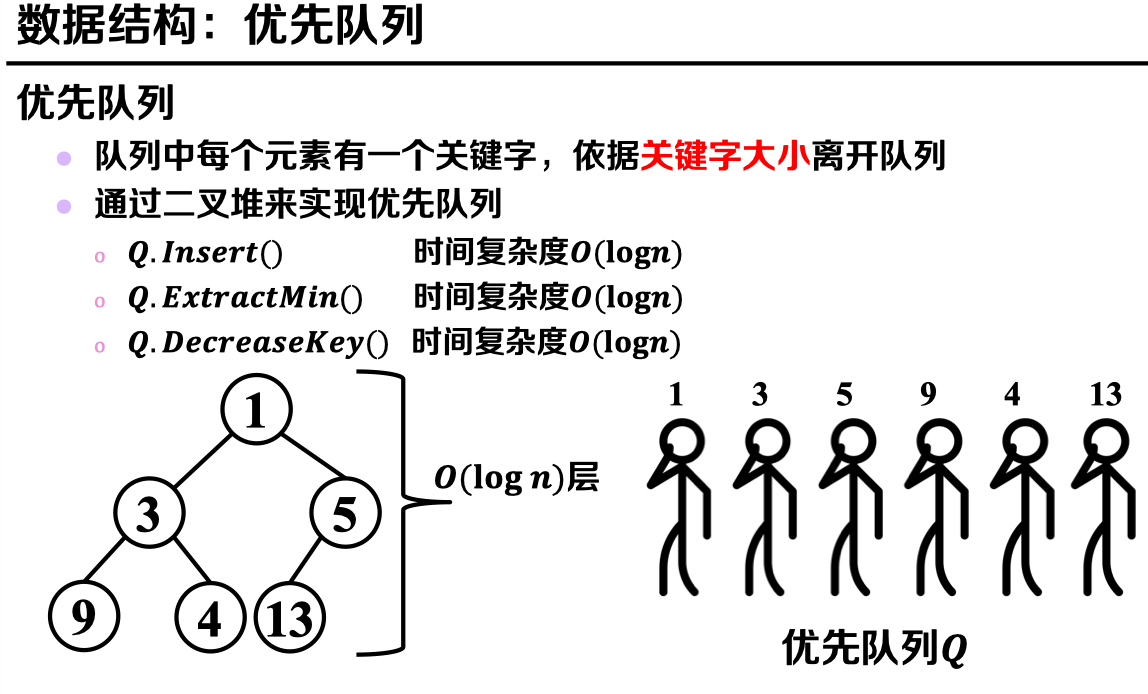
改进后伪代码如下：


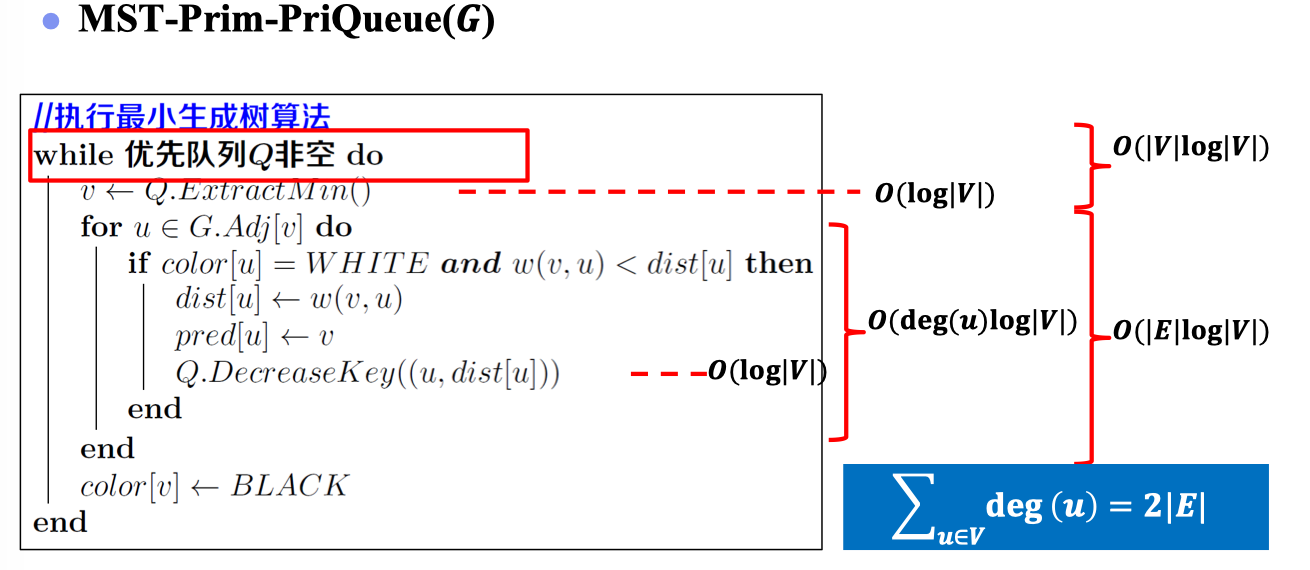
可见，利用优先队列改进后，Prim算法复杂度为O(∣E∣.log∣V∣)O(|E|.log|V|)

2.5 小结：

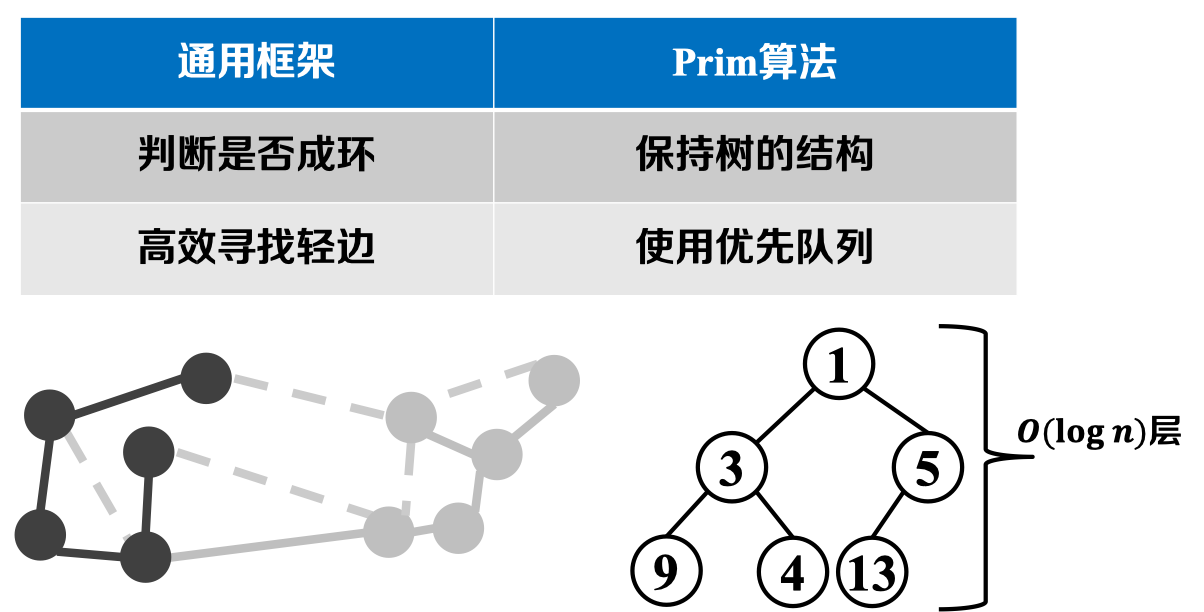
3. Kruskal算法：

Kruskal算法同样是求解最小生成树通用框架策略的一种具体实现。具体而言，该方法主要着眼于“边”的角度。其思想概括如下：

  • 保证无环——每次选边判断是否成环
  • 找轻边——每次选当前权重最小边

3.1 算法思想：

Kruskal算法可以看作是对通用框架的直接实现：

  • 保证所选边集𝑨是一个无环图——选边时避免成环，即：每次选边判断是否成环；
  • 保证所选边集𝑨仍然是最小生成树的子集——每次选择当前权重最小边。

3.2 实例演示：

每次选择未选边中权重最小的边：

...
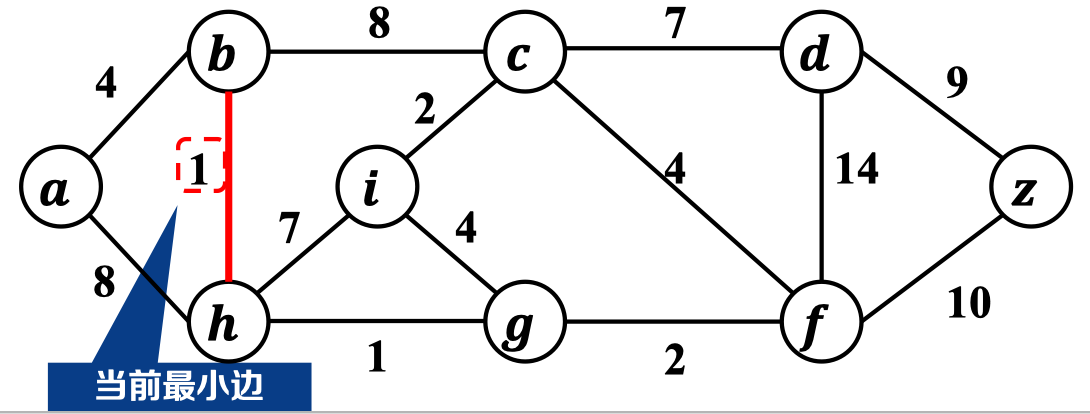
直至此时，仍未成环：

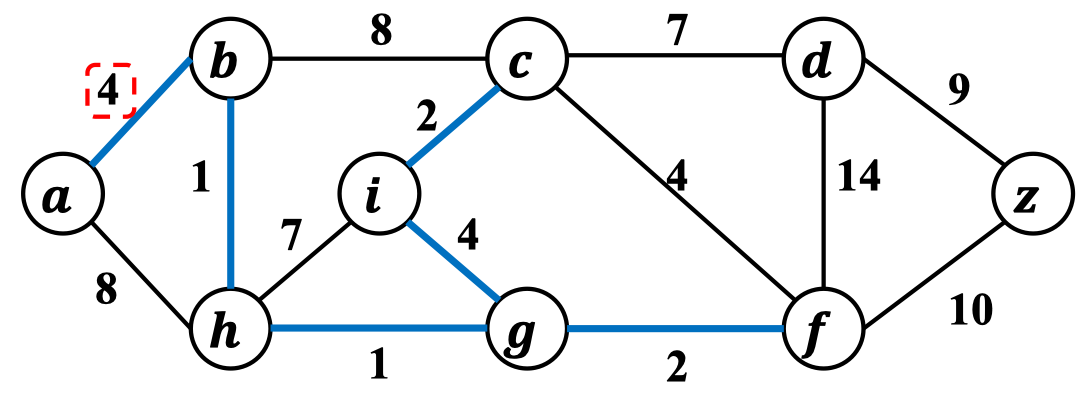
P.s：此时形成多棵子树（森林），而非一棵树。
下一时刻，我们发现——加入当前最小权重边会形成环路，故跳过该边：

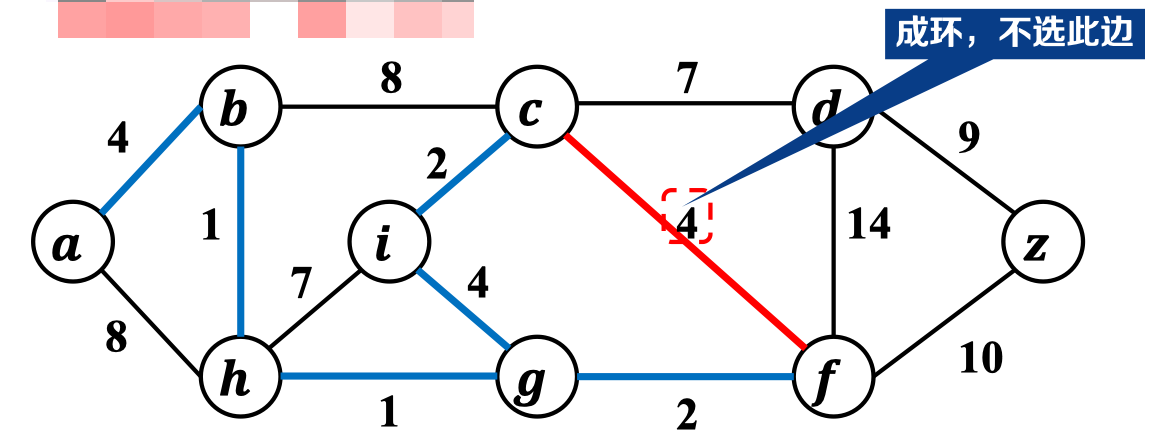
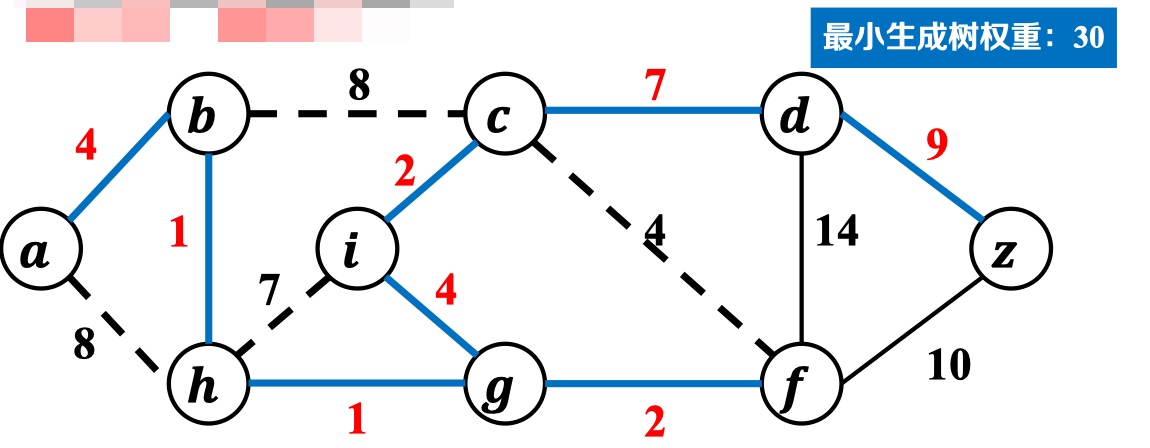
最终，最小生成子树如下：

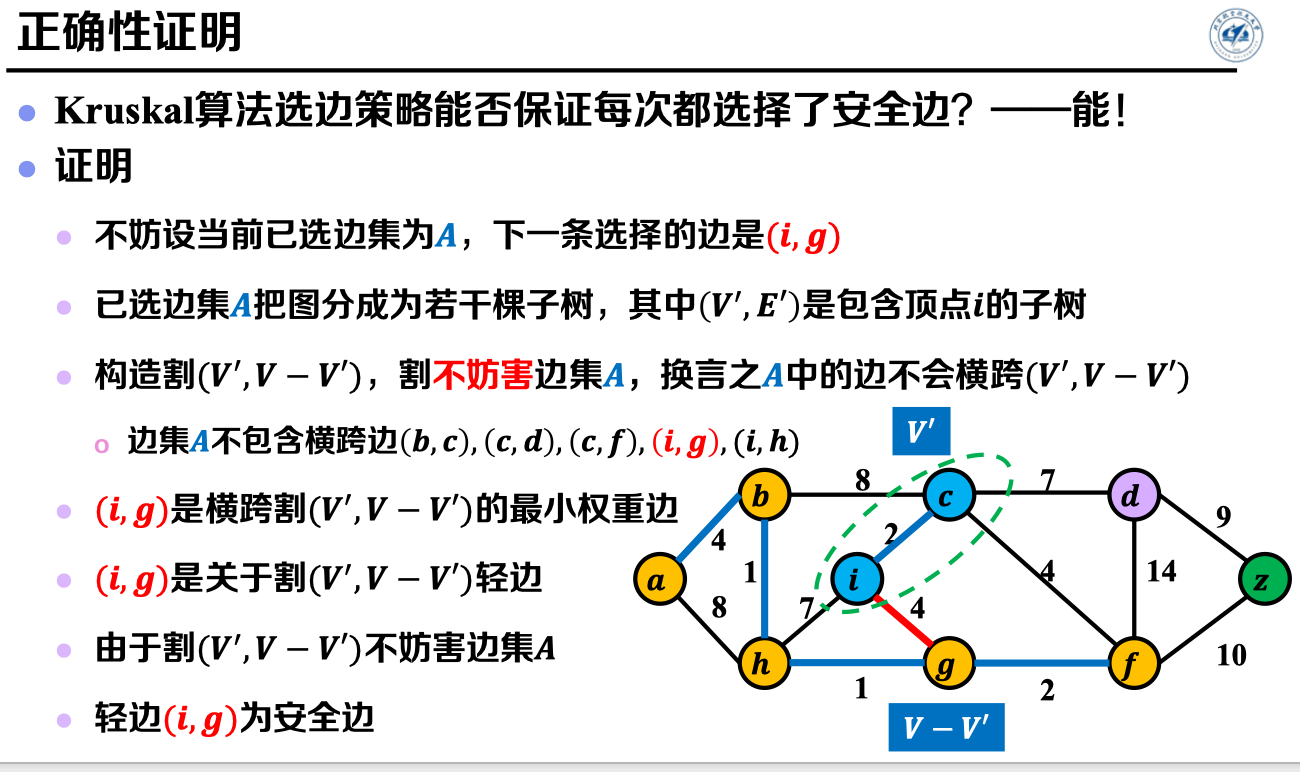
3.3 算法正确性证明：

3.4 算法伪代码：

根据以上伪代码，可见：实现Kruskal算法核心在于如何判断加入边的端点是否位于同一棵子树。此处引入一种很重要的数据结构——并查集（也被称之为“不相交集合”）：

3.5 附加：并查集

并查集是一种可以高效解决“连通性”问题的数据结构。在网上也看到了各种形象化理解并查集的例子，个人感觉最确切的例子可参考：并查集讲解. 简而言之：对于每个查询的元素，指定一个与其同属一个集合的元素作为其代表，若待查询的两个元素其代表相同，则两个元素属于同一集合。并查集主要需要实现以下功能：

  • Create_Set(𝒙)——初始化，初始时，各元素其代表就是自身：
  • Find_Set(𝒙)——查找根节点（代表）：
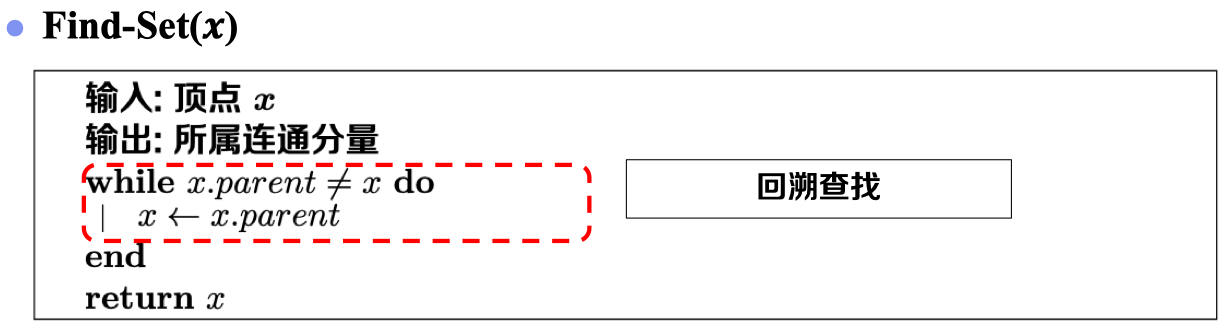
  • Union_Set(𝒙)——合并两组元素：

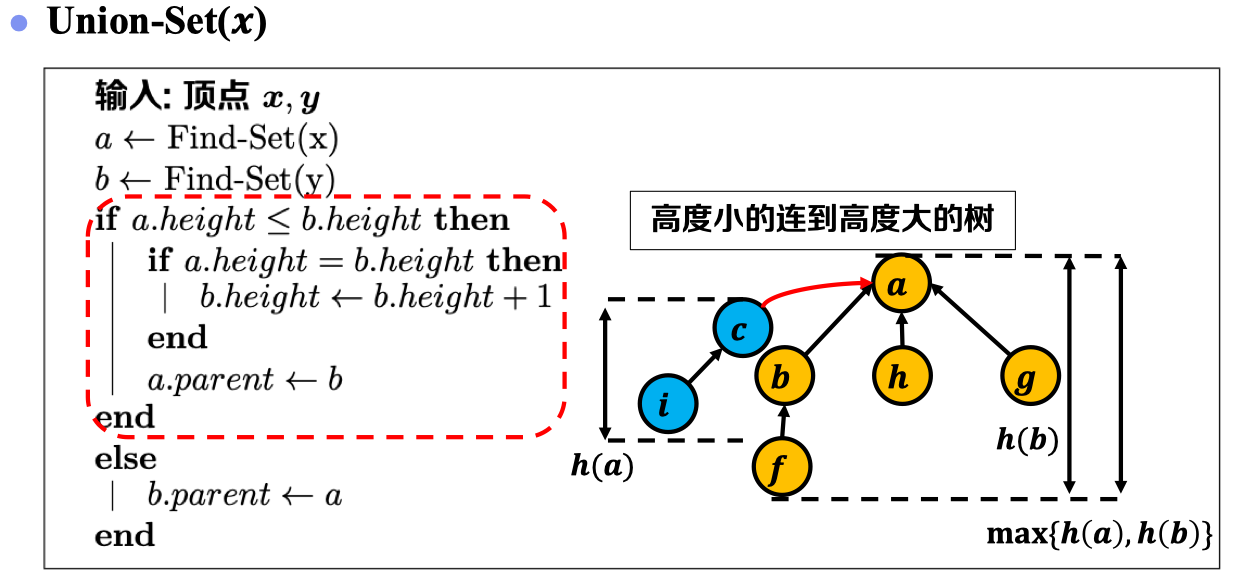
    以上三项功能其时间复杂度均为O(h)O(h)，h为树的高度。树的高度与顶点规模关系可参考以下证明：

3.6 算法具体伪代码：

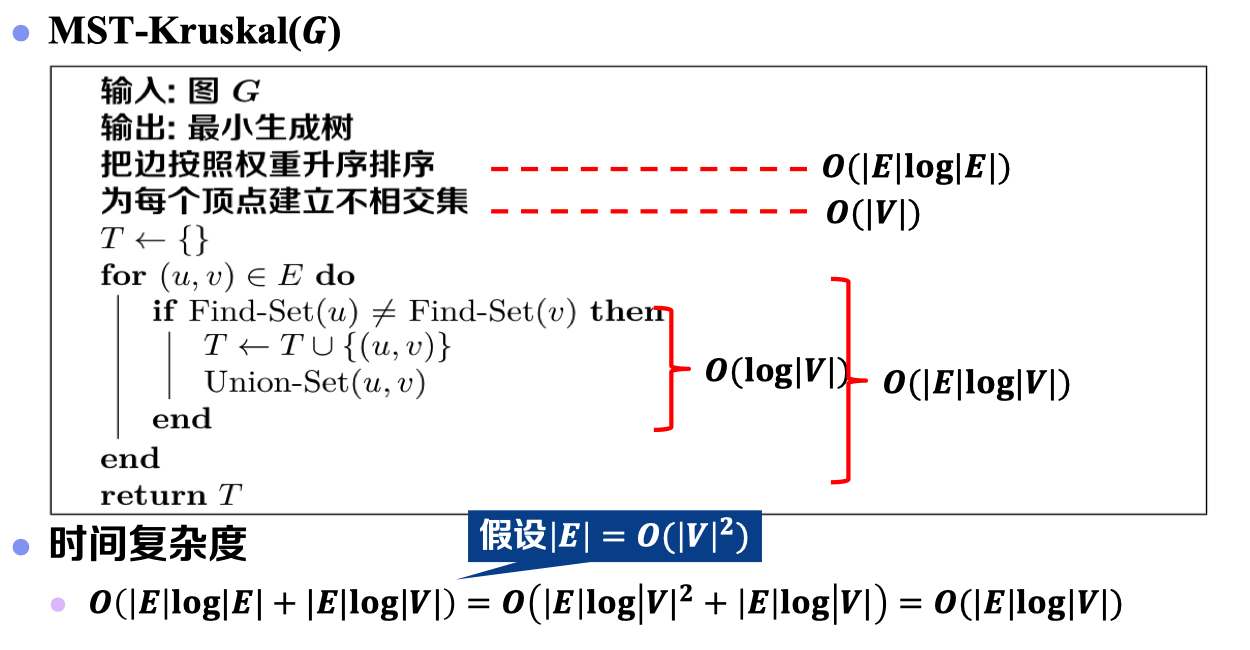
总结：